《2025年一遍过八年级数学上册人教版》

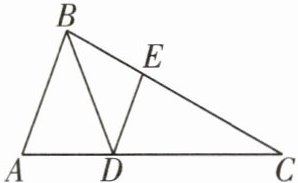
10 [2024汕头潮南区期末]如图,在$\triangle ABC$中,$∠A= 70^{\circ },∠C= 30^{\circ },BD平分∠ABC$交AC于点D,$DE// AB$,交BC于点E,则$∠BDE$的度数是 ( )


A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$

答案： B 在△ABC中,∠A=70°,∠C=30°,
∴∠ABC=180°-∠A-∠C=80°.
∵BD平分∠ABC,
∴∠ABD=$\frac{1}{2}$∠ABC=40°.
∵DE//AB,
∴∠BDE=∠ABD=40°.

11 [2025唐山九中月考]当三角形中一个内角β的度数是另一个内角α的度数的$\frac {1}{2}$时,我们称此三角形为“友好三角形”,这个内角α为“友好角”.如果一个“友好三角形”中有一个内角为$54^{\circ }$,那么这个“友好三角形”的“友好角”的度数为 ( )

A.$108^{\circ }或27^{\circ }$
B.$108^{\circ }或54^{\circ }$
C.$27^{\circ }或54^{\circ }或108^{\circ }$
D.$54^{\circ }或84^{\circ }或108^{\circ }$

答案： D 分三种情况讨论:①若54°角是α,则“友好角”的度数为54°;②若54°角是β,则$\frac{1}{2}$α=β=54°,所以“友好角”的度数为108°;③若54°角既不是α也不是β,则α+β+54°=180°,所以α+$\frac{1}{2}$α+54°=180°,解得α=84°,所以“友好角”的度数为84°.综上,“友好角”的度数为54°或84°或108°.

12 [2025南昌期末]小慧一笔画成了如图所示的图形,若$∠A= 60^{\circ }$,则$∠B+∠C+∠D+∠E$的度数为 ( )

A.$180^{\circ }$
B.$240^{\circ }$
C.$270^{\circ }$
D.$300^{\circ }$

答案： B 如图,设AC,AD分别与BE交于点M,N.在△BCM中,∠B+∠C+∠BMC=180°,
∴∠BMC=180°-(∠B+∠C),
∵∠AMN=∠BMC(对顶角相等),
∴∠AMN=180°-(∠B+∠C).同理可得∠ANM=180°-(∠D+∠E).在△AMN中,∠A+∠AMN+∠ANM=180°,
∴∠A+180°-(∠B+∠C)+180°-(∠D+∠E)=180°,
∴∠B+∠C+∠D+∠E=∠A+180°,
∵∠A=60°,
∴∠B+∠C+∠D+∠E=240°.

13 [2025广州海珠区期末]如图,在三角形纸片ABC中,$∠A= 75^{\circ },∠B= 65^{\circ }$,将纸片的一角沿DE折叠,使点C落在$\triangle ABC内部的点C'$处,若$∠1= 45^{\circ }$,则$∠2= $____$^{\circ }$.

答案： 35° 由折叠的性质,得∠C'DC=2∠CDE,∠C'EC=2∠CED.
∵∠A=75°,∠B=65°,
∴∠C=180°-(65°+75°)=40°,
∴∠CDE+∠CED=180°-∠C=140°,
∴∠C'DC+∠C'EC=2∠CDE+2∠CED=2×140°=280°.
∵∠1+∠C'EC=180°,∠2+∠C'DC=180°,
∴∠1+∠2+∠C'DC+∠C'EC=360°,
∴45°+∠2+280°=360°,
∴∠2=360°-280°-45°=35°.

14 跨学科·物理如图1,光线射向一个平面镜后被反射,两条光线与平面镜的夹角相等(即$∠1= ∠2$).如图2,光线射到平面镜甲上后,又被反射到平面镜乙上,然后光线又被反射到平面镜甲上……若$∠α=55^{\circ },∠γ=75^{\circ }$,则$∠β=$____$^{\circ }$.

答案： 65° 如图,由题意,知∠5=∠α=55°,∠β=∠6,∠3=∠γ=75°.
∵∠5+∠3+∠4=180°,
∴∠4=50°.
∵∠6+∠4+∠β=180°,
∴∠β=65°.

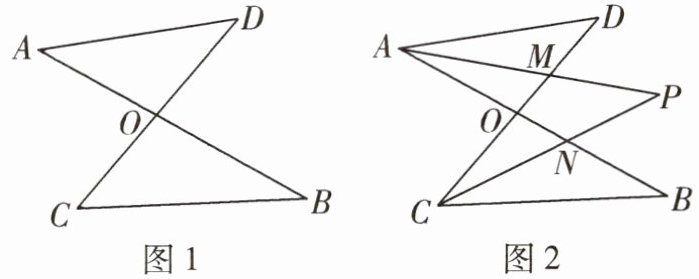
15 推理能力如图1,线段AB,CD相交于点O,连接AD,CB.如图2,在图1的条件下,分别作$∠DAB和∠BCD$的平分线AP,CP,AP,CP相交于点P,且与CD,AB分别相交于点M,N.
(1)在图1中,请直接写出$∠A,∠B,∠C,∠D$之间的数量关系;
(2)在图2中,若$∠D= 40^{\circ },∠B= 30^{\circ }$,求$∠P$的度数;
(3)若图2中$∠D和∠B$为任意锐角,其他条件不变,请直接写出$∠P与∠D,∠B$之间的数量关系.

答案： 解:
(1)∠A+∠D=∠B+∠C.
解法提示:因为∠A+∠D+∠AOD=180°,∠B+∠C+∠BOC=180°,∠AOD=∠BOC,所以∠A+∠D=∠B+∠C.
(2)如图,同
(1)可得∠1+∠D=∠P+∠3,①
∠4+∠B=∠2+∠P.②
因为AP,CP分别为∠DAB和∠BCD的平分线,所以∠1=∠2,∠3=∠4.
由①+②得∠1+∠D+∠4+∠B=∠P+∠3+∠2+∠P,所以∠D+∠B=2∠P.
因为∠D=40°,∠B=30°,
所以2∠P=40°+30°=70°,所以∠P=35°.
(3)∠P=$\frac{1}{2}$(∠B+∠D).
归纳总结
8字型模型
如图,∠A+∠D=∠B+∠C.