《2025年一遍过八年级数学上册人教版》

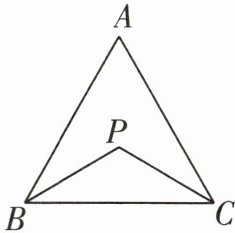
1 教材P17T9变式 如图,在$\triangle ABC$中,点P是$\angle ABC和\angle ACB$的平分线的交点,若$\angle P= 2\angle A$,则$\angle A$的度数为 ( )


A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$

答案： B
∵ 点 P 是∠ABC 和∠ACB 的平分线的交点，
∴∠PBC=$\frac{1}{2}$∠ABC，∠PCB=$\frac{1}{2}$∠ACB，
∴∠P=180°-∠PBC-∠PCB=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A.
∵∠P=2∠A，
∴90°+$\frac{1}{2}$∠A=2∠A，
∴∠A=60°.(模型解法:由模型可知∠P=90°+$\frac{1}{2}$∠A，结合∠P=2∠A，可得∠A=60°)

2 (1)如图,若点P是$\angle ABC,\angle ACB$的三等分线的交点,即$\angle PBC= \frac{1}{3}\angle ABC,\angle PCB= \frac{1}{3}\angle ACB$,则$\angle P与\angle A$的关系为______,证明你的结论.

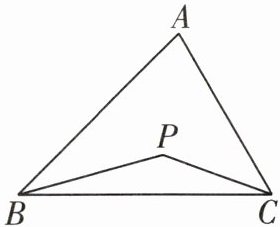
中双角平分线模型
(2)若点P是$\angle ABC,\angle ACB$的四等分线的交点,即$\angle PBC= \frac{1}{4}\angle ABC,\angle PCB= \frac{1}{4}\angle ACB$,则$\angle P与\angle A$的关系为______(直接写出答案,不需要证明).

答案：
(1)∠P=120°+$\frac{1}{3}$∠A 证明:由三角形的内角和定理，得∠ABC+∠ACB=180°-∠A.
∵∠PBC=$\frac{1}{3}$∠ABC，∠PCB=$\frac{1}{3}$∠ACB，
∴∠PBC+∠PCB=$\frac{1}{3}$(∠ABC+∠ACB)=$\frac{1}{3}$(180°-∠A)=60°-$\frac{1}{3}$∠A，
∴∠P=180°-(∠PBC+∠PCB)=180°-60°+$\frac{1}{3}$∠A=120°+$\frac{1}{3}$∠A，
∴∠P 与∠A 的关系为∠P=120°+$\frac{1}{3}$∠A.
(2)∠P=135°+$\frac{1}{4}$∠A

3 [2025西南大学附属中学开学考试]如图,$\triangle ABC$为直角三角形,$\angle ACB= 90^{\circ}$,AD为$\angle CAB$的平分线,与$\angle ABC$的平分线BE交于点E,BG是$\triangle ABC$的外角平分线,AD与BG相交于点G,则$\angle ADC与\angle GBF$的度数和为 ( )

A.$120^{\circ}$
B.$135^{\circ}$
C.$150^{\circ}$
D.$160^{\circ}$

答案： B
∵∠ACB=90°，
∴∠CAB+∠CBA=90°.
∵AE，BE 分别平分∠CAB，∠CBA，
∴∠BED=∠EAB+∠EBA=$\frac{1}{2}$∠CAB+$\frac{1}{2}$∠CBA=45°.
∵BG 平分∠CBF，
∴∠CBG=$\frac{1}{2}$∠CBF.
∵∠CBE=$\frac{1}{2}$∠CBA，
∴∠GBE=∠CBG+∠CBE=$\frac{1}{2}$∠CBF+$\frac{1}{2}$∠CBA=90°，
∴∠G=90°-∠BEG=90°-45°=45°.
∵∠ADC=∠BDG，
∴∠ADC+∠GBF=∠BDG+∠DBG=180°-∠G=135°.(模型解法:由一内角一外角平分线模型可得∠G=$\frac{1}{2}$∠C=45°，
∴∠ADC+∠GBF=∠BDG+∠GBD=180°-∠G=135°)

4 [2025成都成华区期末]如图,点E是$\triangle ABC的外角\angle CBD$内部一点,满足$\angle CAB= 3\angle EAB,\angle CBD= 3\angle EBD$.若$\angle C= 42^{\circ}$,则$\angle E$的度数是______.

答案： 14° 设∠EAB=x，∠EBD=y，
∵∠CAB=3∠EAB，∠CBD=3∠EBD，
∴∠CAB=3x，∠CBD=3y，
∵∠C=∠CBD-∠CAB=3y-3x=42°，
∴y-x=14°，
∴∠E=∠EBD-∠EAB=y-x=14°.

5 如图,在$\triangle ABC$中,$\angle A= 64^{\circ},\angle ABC与\angle ACD的平分线交于点A_1$,则$\angle A_1$的度数为______;$\angle A_1BC与\angle A_1CD的平分线交于点A_2$……$$依次进行下去,$\angle A_{n-1}BC与\angle A_{n-1}CD的平分线相交于点A_n$,要使$\angle A_n的度数小于1^{\circ}$,则n的最小值为______.

答案： 32° 7
∵∠ABC 的平分线与∠ACD 的平分线交于点A₁，
∴∠A₁BC=$\frac{1}{2}$∠ABC，∠A₁CD=$\frac{1}{2}$∠ACD.由三角形外角的性质，得∠A₁=∠A₁CD-∠A₁BC=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$∠A，
∴∠A₁=$\frac{1}{2}$∠A=32°.同理可得∠A₂=$\frac{1}{4}$∠A，…，∠Aₙ=($\frac{1}{2}$)ⁿ∠A=$\frac{64°}{2ⁿ}$.当∠Aₙ的度数为1°时，n=6.
∵∠Aₙ的度数小于1°，
∴n 的最小值为7.