《2025年一遍过八年级数学上册人教版》

7 [2025宿迁沭阳期中]如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,最省事的做法是带碎片( )

A.①
B.②
C.③
D.①③

答案： C 由题图可知,③有完整的两角与夹边,根据“ASA”可以得到与原三角形模具全等的三角形,所以最省事的做法是带③去.

8 [2025石家庄九中期中]如图,$AB⊥CD$,且$AB= CD$,$CE⊥AD于点E$,$BF⊥AD于点F$.若$CE= 8$,$BF= 4$,$EF= 3$,则$AD$的长为( )

A.9
B.8
C.7
D.6

答案： A 设 AB 与 CD 交于点 G.
∵ CE⊥AD,AB⊥CD,BF⊥AD,
∴ ∠CED=∠AGD=∠AFB=90°,
∴ ∠C + ∠D = ∠A + ∠D = 90°,
∴ ∠A = ∠C. 在△CED 和△AFB 中,∠C=∠A,∠CED=∠AFB,CD=AB,
∴ △CED≌△AFB(AAS),
∴ AF=CE=8,DE=BF=4,
∴ DF=DE - EF = 1,
∴ AD=AF + DF = 9.

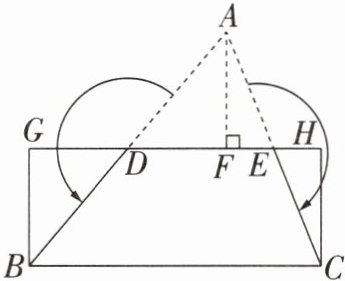
9 [新趋势·数学文化][2025洛阳市第二外国语学校月考]中国古代数学家刘徽在《九章算术注》中,给出证明三角形面积公式的出入相补法.如图所示,在$\triangle ABC$中,分别取$AB$,$AC的中点D$,$E$,连接$DE$,过点$A作AF⊥DE$,垂足为$F$,将$\triangle ABC分割后拼接成长方形BCHG$.若$DE= 5$,$AF= 4$,则$\triangle ABC$的面积是______.

答案： 40 解题思路:证明△ADF≌△BDG(AAS),△AFE≌△CHE(AAS),求出 GH 和 CH,根据△ABC 和长方形 BCHG的面积相等进行求解.

10 [2025抚顺东洲区期末]如图,$∠ACB= 90^{\circ }$,$AC= BC$,$AD⊥CE$,$BE⊥CE$,垂足分别为$D$,$E$.
(1)求证：$AD= CE$.

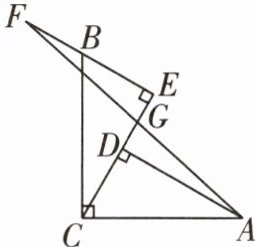
(2)延长$EB至点F$,使得$BF= DE$,连接$AF交CE于点G$.若$AD= 9$,$BE= 5$,求$\triangle EFG$的面积.

答案：
(1)证明:
∵ ∠ACB=90°,AD⊥CE,BE⊥CE,
∴ ∠ADC=∠E=90°,∠ACD + ∠BCE = 90°,
∴ ∠ACD + ∠DAC = 90°,
∴ ∠DAC=∠BCE.在△ACD 和△CBE 中,∠ADC=∠E,∠DAC=∠ECB,AC=CB,
∴ △ACD≌△CBE(AAS),
∴ AD=CE.
(2)解:
∵ △ACD≌△CBE,
∴ CE=AD=9,CD=BE=5,
∴ DE=CE - CD = 4.
∵ BF=DE,BE=CD,
∴ BF + BE = DE + CD,即 EF=CE,
∴ EF=AD=9.在△ADG 和△FEG 中,∠ADG=∠E,∠DGA=∠EGF,AD=FE,
∴ △ADG≌△FEG(AAS),
∴ DG=EG,
∴ EG = $\frac{1}{2}$DE = 2,
∴ S△EFG = $\frac{1}{2}$EG·EF = 9.

11 [推理能力][2024湖州吴兴区期中]在$\triangle ABC$中,点$D在直线AB$上,点$F在BC$的延长线上,$∠E= ∠BDC$,$AE= CD$,$∠EAB+∠DCF= 180^{\circ }$.
(1)如图1,求证：$AD+BC= BE$.
(2)如图2、图3,请分别写出线段$AD$,$BC$,$BE$之间的数量关系,不需要证明.

答案：
(1)证明:
∵ ∠EAB + ∠DCF = 180°,∠DCB + ∠DCF = 180°,
∴ ∠EAB=∠DCB.在△EAB 和△DCB 中,∠E=∠BDC,AE=CD,∠EAB=∠DCB,
∴ △EAB≌△DCB(ASA),
∴ BE=BD,AB=BC,
∴ AD + BC = AD + AB = BD = BE,即 AD + BC = BE.
(2)解:题图2结论:BC - AD = BE.题图3结论:AD - BC = BE.解题通法解决类比探究问题的方法
(1)根据题干条件,结合分支条件,解决第一问,并梳理框架;
(2)类比第一问的方法解决下一问.整体框架照搬,类比辅助线、类比思路;
(3)对比不同分支条件,确定变和不变,得出结论.

12 [几何直观][2025景德镇期末]如图,在$4×4$的正方形网格图中,线段$AB$的端点都在格点上,请按要求用无刻度的直尺作图.

(1)在图1中作格点线段$CD⊥AB$,垂足为$E$；
(2)在图2中的线段$AB上作点H$,使得$AH= BH$.

答案： 解:
(1)如图1,线段 CD,AB 与 CD 的交点 E 即为所求(答案不唯一).(点拨:在正方形网格中作垂线,可通过构造两个直角三角形全等来解)解法提示:连接 AF,FB,DG.在△ABF 和△DCG 中,BF=CG,∠AFB=∠DGC,AF=DG,
∴ △ABF≌△DCG(SAS),
∴ ∠BAF=∠CDG,∠ABF=∠DCG.
∵ ∠ABF + ∠BAF = 90°,
∴ ∠DCG + ∠BAF = 90°,
∴ ∠AEC = 180° - (∠DCG + ∠BAF) = 180° - 90° = 90°,
∴ DE⊥AB.
(2)如图2,点 H 即为所求.解法提示:连接 AD,BC,CD,CD 与 AB 交于点 H.
∵ AD//BC,
∴ ∠DAH=∠CBH,∠ADH=∠BCH.在△ADH 和△BCH 中,∠DAH=∠CBH,AD=BC,∠ADH=∠BCH,
∴ △ADH≌△BCH(ASA),
∴ AH=BH,
∴ 点 H 即为所求.