第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
10 教材P9T4变式 [2025南充嘉陵区期末]如图,CD,CE,CF分别是$ \triangle ABC $的高、角平分线、中线,则下列各式错误的是 ( )
A.$ AB = 2BF $
B.$ \angle ACE = \frac{1}{2} \angle ACB $
C.$ AE = BE $
D.$ CD \perp BE $
A.$ AB = 2BF $
B.$ \angle ACE = \frac{1}{2} \angle ACB $
C.$ AE = BE $
D.$ CD \perp BE $
答案:
C
∵ CD,CE,CF 分别是△ABC 的高、角平分线、中线,
∴ CD⊥BE,$\angle ACE=\frac{1}{2}\angle ACB$,AB=2BF,
∴ A,B,D 正确,C 错误
∵ CD,CE,CF 分别是△ABC 的高、角平分线、中线,
∴ CD⊥BE,$\angle ACE=\frac{1}{2}\angle ACB$,AB=2BF,
∴ A,B,D 正确,C 错误
11 [2025三门峡灵宝期中]如图,AD为$ \triangle ABC $的中线,DE,DF分别为$ \triangle ADB $,$ \triangle ADC $的高. 若$ AB = 3 $,$ AC = 4 $,$ DF = 1.5 $,则$ DE = $____.
答案:
2
∵ AD 为△ABC 的中线,
∴ BD=DC,
∴$S_{\triangle ABD}=S_{\triangle ADC}$,
∵ DE,DF 分别是△ABD,△ADC 的高,$\therefore \frac{1}{2}AB\cdot DE=\frac{1}{2}AC\cdot DF$,
∵ AB=3,AC=4,DF=1.5,$\therefore \frac{1}{2}×3× DE=\frac{1}{2}×4×1.5$,
∴ DE=2.
∵ AD 为△ABC 的中线,
∴ BD=DC,
∴$S_{\triangle ABD}=S_{\triangle ADC}$,
∵ DE,DF 分别是△ABD,△ADC 的高,$\therefore \frac{1}{2}AB\cdot DE=\frac{1}{2}AC\cdot DF$,
∵ AB=3,AC=4,DF=1.5,$\therefore \frac{1}{2}×3× DE=\frac{1}{2}×4×1.5$,
∴ DE=2.
12 推理能力 数学活动课上,老师提出了如下问题:如图,在$ \triangle ABC $中,$ AB = AC $,P是BC上一点,过点P作$ PD \perp AB $,$ PE \perp AC $,垂足分别为D,E,过点B作$ BF \perp AC $,垂足为F,连接AP.
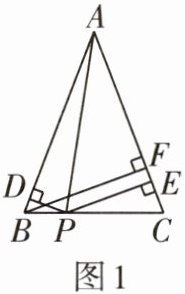
(1)如图1,当P为BC边上的任意一点时,线段PD,PE,BF之间的数量关系是什么?并说明理由.
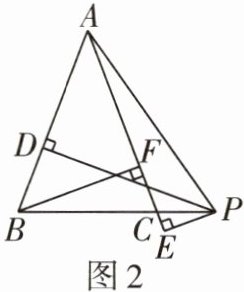
(2)如图2,当点P在BC边的延长线上时.
①试猜想(1)中的数量关系是否仍然成立? 若成立,请加以证明;若不成立,请写出成立的数量关系,并说明理由.
②当$ S_{\triangle ABC} = 10 $,$ AB = 5 $,$ PE = 2 $时,线段PD的长为____.


(1)如图1,当P为BC边上的任意一点时,线段PD,PE,BF之间的数量关系是什么?并说明理由.
(2)如图2,当点P在BC边的延长线上时.
①试猜想(1)中的数量关系是否仍然成立? 若成立,请加以证明;若不成立,请写出成立的数量关系,并说明理由.
②当$ S_{\triangle ABC} = 10 $,$ AB = 5 $,$ PE = 2 $时,线段PD的长为____.
答案:
解:
(1)BF=PD+PE.理由如下:
∵ 点 P 在线段 BC 上,
∴$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,$\therefore \frac{1}{2}AC\cdot BF=\frac{1}{2}AB\cdot PD+\frac{1}{2}AC\cdot PE$.
∵ AB=AC,
∴ BF=PD+PE.
(2)①
(1)中的数量关系不成立.BF=PD-PE.理由:
∵ 点 P 在 BC 的延长线上,
∴$S_{\triangle ABC}=S_{\triangle ABP}-S_{\triangle ACP}$,$\therefore \frac{1}{2}AC\cdot BF=\frac{1}{2}AB\cdot PD-\frac{1}{2}AC\cdot PE$.
∵ AB=AC,
∴ BF=PD-PE.
② 6 解法提示:
∵$S_{\triangle ABC}=\frac{1}{2}AC\cdot BF=10$,AB=AC=5,$\therefore \frac{1}{2}×5× BF=10$,
∴ BF=4.由①可知 PD=BF+PE,
∴ PD=4+2=6.
(1)BF=PD+PE.理由如下:
∵ 点 P 在线段 BC 上,
∴$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,$\therefore \frac{1}{2}AC\cdot BF=\frac{1}{2}AB\cdot PD+\frac{1}{2}AC\cdot PE$.
∵ AB=AC,
∴ BF=PD+PE.
(2)①
(1)中的数量关系不成立.BF=PD-PE.理由:
∵ 点 P 在 BC 的延长线上,
∴$S_{\triangle ABC}=S_{\triangle ABP}-S_{\triangle ACP}$,$\therefore \frac{1}{2}AC\cdot BF=\frac{1}{2}AB\cdot PD-\frac{1}{2}AC\cdot PE$.
∵ AB=AC,
∴ BF=PD-PE.
② 6 解法提示:
∵$S_{\triangle ABC}=\frac{1}{2}AC\cdot BF=10$,AB=AC=5,$\therefore \frac{1}{2}×5× BF=10$,
∴ BF=4.由①可知 PD=BF+PE,
∴ PD=4+2=6.
1 [2025 广州知用学校期中]如图,在$\triangle ABC$中,$D,E,F分别是AC,BD,AE$的中点,若$\triangle DEF的面积为1$,则$\triangle ABC$的面积是 ( )
A.$3$
B.$4$
C.$8$
D.$12$
用——面积问题 答案 P03
A.$3$
B.$4$
C.$8$
D.$12$
用——面积问题 答案 P03
答案:
C
∵ D,E,F 分别是 AC,BD,AE 的中点,
∴ S△ADE=2S△DEF,S△ABD=2S△ADE,S△ABC=2S△ABD,
∴ S△ABC=8S△DEF=8.
∵ D,E,F 分别是 AC,BD,AE 的中点,
∴ S△ADE=2S△DEF,S△ABD=2S△ADE,S△ABC=2S△ABD,
∴ S△ABC=8S△DEF=8.
2 如图,$CD是AB$边上的中线,$BE是CD$边上的中线,$F为DE$的中点. 若$\triangle ADF的面积为2$,则$\triangle ABC$的面积为 ( )
A.$12$
B.$14$
C.$16$
D.$18$
A.$12$
B.$14$
C.$16$
D.$18$
答案:
C 如图,连接 AE.
∵ F 为 DE 的中点,△ADF 的面积为 2,
∴ S△ADE=2S△ADF=2×2=4.
∵ BE 是 CD 边上的中线,
∴ DE=CE,
∴ AE 是 CD 边上的中线,
∴ S△ACD=2S△ADE=2×4=8.
∵ CD 是AB 边上的中线,
∴ S△ABC=2S△ACD=2×8=16.
C 如图,连接 AE.
∵ F 为 DE 的中点,△ADF 的面积为 2,
∴ S△ADE=2S△ADF=2×2=4.
∵ BE 是 CD 边上的中线,
∴ DE=CE,
∴ AE 是 CD 边上的中线,
∴ S△ACD=2S△ADE=2×4=8.
∵ CD 是AB 边上的中线,
∴ S△ABC=2S△ACD=2×8=16.

3 如图,点$G为\triangle ABC$的重心,$D,E,F分别为BC,CA,AB$的中点,具有性质:$AG:GD= BG:GE= CG:GF= 2:1$. 已知$\triangle AFG的面积为3$,则$\triangle ABC$的面积为____.
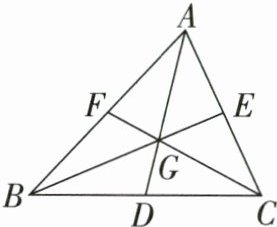

答案:
18
∵ CG:GF=2:1,S△AFG=3,
∴ S△ACG=6,
∴ S△ACF=3+6=9.
∵ F 为 AB 的中点,
∴ S△ABC=2S△ACF=18.
∵ CG:GF=2:1,S△AFG=3,
∴ S△ACG=6,
∴ S△ACF=3+6=9.
∵ F 为 AB 的中点,
∴ S△ABC=2S△ACF=18.
查看更多完整答案,请扫码查看


