《2025年一遍过八年级数学上册人教版》

10 教材P31T2变式 [2025大连沙河口区期末]如图,点D,E在$△ABC$的边BC上,$△ABD\cong △ACE$,其中B,C为对应顶点,D,E为对应顶点,下列结论不一定成立的是 ( )

A.$AC= CD$
B.$BE= CD$
C.$∠ADE= ∠AED$
D.$∠BAE= ∠CAD$

答案： A

11 [2025武威八中期中]如图,$AD是△ABC$的高,点F是AD上一点,连接CF,若$△ABD\cong △CFD$,点B和点F,点A和点C是对应顶点,$DC= 6,DF= 2$,则$△ABC$的面积为( )

A.48
B.24
C.18
D.12

答案： B
∵△ABD≌△CFD，DC = 6，DF = 2，
∴AD = DC = 6，BD = DF = 2，
∴BC = BD + DC = 8。
∵AD是△ABC的高，
∴△ABC的面积为$\frac{1}{2}$BC·AD = $\frac{1}{2}$×8×6 = 24。

12 [2025重庆梁平区期末]已知一个三角形的三边长分别为5,7,x,另一个三角形的三边长分别为y,7,6,若这两个三角形全等,则$x-y= $____.

答案： 1 若这两个三角形全等，则x = 6，y = 5(点拨:全等三角形的对应边相等)，
∴x - y = 1。

13 [2025济南钢城区期末]如图,在平面直角坐标系中,点A,B的坐标分别是$(-6,0),(0,4),△OA'B'\cong △AOB$,点$B'$和点B是对应顶点,$OB'$和AB是对应边.若点$A'$在x轴上,则点$B'$的坐标是____.

答案： (6, - 4)
∵点A(- 6, 0)，B(0, 4)，
∴OA = 6，OB = 4。
∵△OA'B'≌△AOB，
∴OA' = OA = 6，A'B' = OB = 4，
∴点B'的坐标是(6, - 4)。

14 [2025衢州柯城区期末]如图,$△ABD\cong △ACD,∠B和∠C,∠BDA和∠CDA$是对应角,$BD,AC$的延长线交于点E.若$AE= 7,AB= 5,BE= 4$,则$△CDE$的周长为____.

答案： 6
∵△ABD≌△ACD，
∴AC = AB = 5，CD = BD。
∵AE = 7，
∴CE = AE - AC = = 2
∵BE = 4，
∴△CDE的周长为CD + DE + CE = BD + DE + CE = BE + CE = 6。

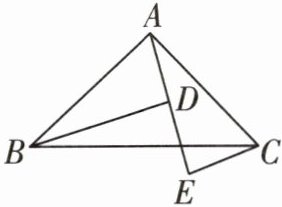
15 [2025菏泽成武期中]如图,A,D,E三点在同一条直线上,且$△BAD\cong △ACE$,点D和点E,点A和点C是对应顶点,连接BC.
(1)求证:$BD= DE+CE$.
(2)探究当$∠ADB$满足什么条件时,$BD// CE$?并说明理由.

答案：
(1)证明:
∵△BAD≌△ACE，
∴BD = AE，AD = CE，
∴BD = AE = AD + DE = CE + DE，
即BD = DE + CE；
(2)解:当∠ADB = 90°时，BD//CE。
理由:
∵△BAD≌△ACE，
∴∠E = ∠ADB。
∵∠ADB = 90°，
∴∠BDE = 180° - ∠ADB = 90°，∠E = 90°，
∴∠BDE = ∠E，
∴BD//CE。

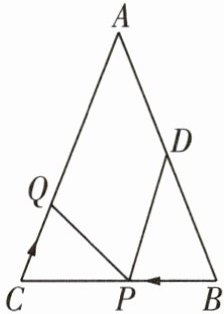
16 推理能力 [2025石家庄一中期中]如图,在$△ABC$中,$∠B= ∠C,AB= 16,BC= 12$,点D为AB的中点,点P在线段BC上以每秒3个单位长度的速度由点B向点C运动,同时点Q在线段CA上以每秒a个单位长度的速度由点C向点A运动,设运动时间为t(秒)$(0≤t≤4)$.
(1)用含t的代数式表示线段PC的长;
(2)若点P,Q的运动速度不相等,但某个时刻$△BPD与△CQP$全等,求a的值.

答案： 解:
(1)
∵BC = 12，点P在线段BC上以每秒3个单位长度的速度由点B向点C运动，
∴BP = 3t，
∴PC = BC - BP = 12 - 3t。
(2)
∵AB = 16，点D为AB的中点，
∴BD = $\frac{1}{2}$AB = 8。
∵点P，Q的运动速度不相等，
∴BP≠CQ。
又
∵△BPD与△CQP全等，∠B = ∠C，
∴BP = PC，BD = CQ，
∴3t = 12 - 3t，8 = at，
解得t = 2，a = 4，即a的值为4。