《2025年一遍过八年级数学上册人教版》

1 从图1和图2中分别找出两组全等形.(不添加其他字母及辅助线)

答案： 解:题图1中,全等三角形有△ANM≌△BPN,△ACE≌△BDF.(答案不唯一)
题图2中,全等三角形有△EFO≌△BCO,△DEO≌△ABO.

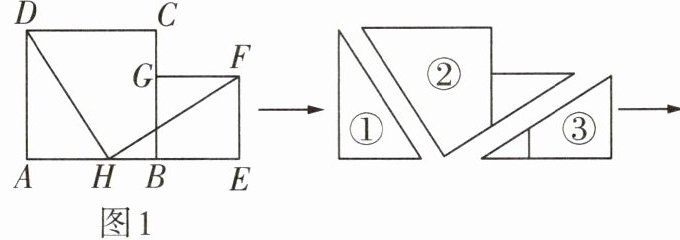
2 把两个边长不等的正方形卡纸ABCD与BEFG如图1所示摆放(点A,B,E在同一条直线上,AB＞BE),点H是边AB上一点,连接DH,HF,沿DH,HF裁剪成①②③三块,拼接成如图2所示的一个正方形图案.
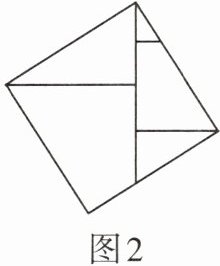
(1)若$S_{正方形ABCD}= 7 cm^2,S_{正方形BEFG}= 3 cm^2,$则图2中正方形图案的面积为______cm^2.
(2)试根据题意判断△ADH与△EHF是否全等?并说明理由.

答案： 解:
(1)10
(2)△ADH≌△EHF.理由如下:
由将①②③拼接成一个正方形图案可知DH⊥FH,DH=FH.
∵在正方形ABCD和正方形BEFG中,∠DAH=∠FEH=90°,
∴∠AHD+∠ADH=∠AHD+∠EHF=90°,
∴∠ADH=∠EHF.
在△ADH和△EHF中,{∠DAH=∠HEF,∠ADH=∠EHF,DH=HF,
∴△ADH≌△EHF(AAS).

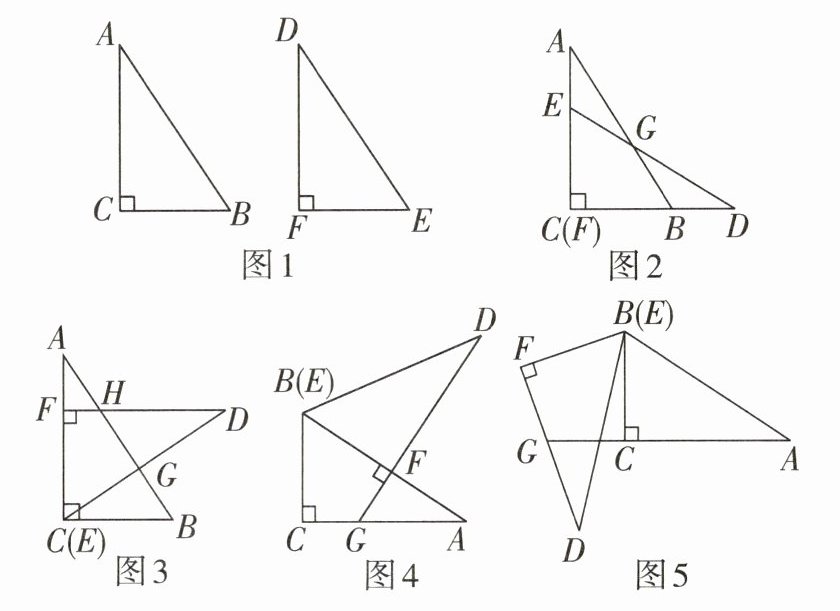
3 如图1是两张三角形纸片,已知Rt△ABC≌Rt△DEF,其中∠ACB= ∠DFE= 90°.
(1)若将这两张三角形纸片按如图2方式摆放,使点C与点F重合,AB交DE于点G,写出图中的全等三角形(不包括△ABC≌△DEF),并说明理由.
(2)若将这两张三角形纸片按如图3方式摆放,使点C与点E重合,AB与DF,DE分别交于点H、点G,试判断AB与CD的位置关系,并说明理由.
(3)若将这两张三角形纸片按如图4方式摆放,使点B与点E重合,点F落在AB上,DF的延长线交AC于点G.写出此时AG,FG与DF之间的数量关系,并说明理由.
(4)若将这两张三角形纸片按如图5方式摆放,使点B与点E重合,AC的延长线交DF于点G.(3)中的结论还成立吗?若成立,写出证明过程;若不成立,请直接写出AG,FG与DF之间的数量关系.

答案：
解:
(1)△AGE≌△DGB.理由如下:
∵Rt△ABC≌Rt△DEF,
∴∠A=∠D,AC=DF,BC=EF,
∴AC - EF=DF - BC,即AE=DB.
在△AGE和△DGB中,{∠A=∠D,∠AGE=∠DGB,AE=DB,
∴△AGE≌△DGB(AAS).
(2)AB⊥CD.理由如下:
∵Rt△ABC≌Rt△DEF,
∴∠A=∠D.
∵∠DFC=∠ACB=90°,
∴DF//BC,
∴∠D=∠BCG,
∴∠A=∠BCG,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠BCG+∠B=90°,
∴∠BGC=90°,
∴AB⊥CD.
(3)DF=AG+FG.理由如下:
如图,连接BG.
∵Rt△ABC≌Rt△DEF,
∴BC=EF,AC=DF.
在Rt△BCG和Rt△BFG中,{BG=BG,BC=BF,
∴Rt△BCG≌Rt△BFG(HL),
∴FG=CG,
∴DF=AC=AG+CG=AG+FG.

(4)
(3)中的结论不成立,应是AG=DF+FG.
解法提示:如图,连接BG.
∵Rt△ABC≌Rt△DEF,
∴EF=BC,AC=DF.
在Rt△BCG和Rt△BFG中,{BG=BG,BC=BF,
∴Rt△BCG≌Rt△BFG(HL),
∴CG=FG,
∴AG=AC+CG=DF+FG.