《2025年一遍过八年级数学上册人教版》

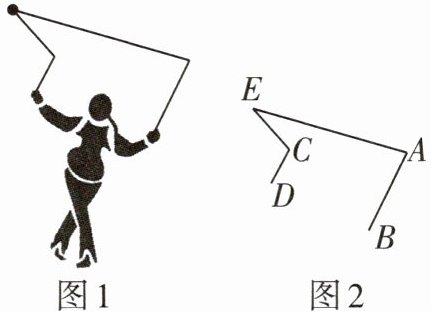
10 新趋势·传统文化 [2025鞍山模拟]为增强学生体质,学校将“抖空竹”引入体育社团. 图1是“抖空竹”时的一个瞬间,小明把它抽象成图2的数学问题：已知AB // CD,∠E = 30°,∠ECD = 110°,则∠A的度数是( )


A.60°
B.70°
C.80°
D.90°

答案：
C 如图，延长DC，交AE于点F。
∵∠E=30°，∠ECD=110°，
∴∠EFC=∠ECD−∠E=110°−30°=80°。
∵AB//CD，
∴∠A=∠EFC=80°。

11 [2025宁波精准联盟期中]如图,将一张三角形纸片ABC沿DE折叠,使点A落在△ABC外的点A'处. 如果∠A = α,∠CEA' = β,∠BDA' = γ,那么下列式子中正确的是( )


A.γ = 2α + β
B.γ = α + 2β
C.γ = α + β
D.γ = 180° - α - β

答案：
A 如图，设AC与A'D交于点F。由折叠得∠A=∠A'。
∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，∠A=α，∠CEA'=β，∠BDA'=γ，
∴γ=α+α+β=2α+β。

12 一题多解 一个零件的形状如图所示,按规定∠A应等于90°,∠B,∠C分别为21°和32°. 检验工人量得∠BDC = 148°,就断定这个零件不合格,这是为什么？

答案：
解:通解 如图1，延长CD交AB于点E。
∵工人量得∠BDC=148°，
∴∠BDE=180°−∠BDC=180°−148°=32°。
∵∠B=21°，
∴∠AEC=∠B+∠BDE=21°+32°=53°。
∵∠C=32°，
∴∠A=180°−∠C−∠AEC=95°≠90°，
∴这个零件不合格。另解 如图2，连接AD并延长，则∠1=∠C+∠DAC，∠2=∠B+∠DAB。假设这个零件合格，则∠BAC=90°。
∵∠B=21°，∠C=32°，
∴∠BDC=∠1+∠2=∠C+∠DAC+∠B+∠DAB=∠B+∠BAC+∠C=143°≠148°，
∴这个零件不合格。巧解 如图3，连接BC。假设这个零件合格，则∠A=90°。
∵∠ABD=21°，∠ACD=32°，
∴∠BCD+∠CBD=180°−90°−21°−32°=37°，
∴∠BDC=180°−(∠BCD+∠CBD)=143°≠148°，
∴这个零件不合格。

13 教材P17T11变式 [2025福州仓山区期末]如图,在△ABC中,点D在BC的延长线上,延长BA至点E,连接EC. 设∠B = α,∠E = β,若∠BAC = α + 2β,求证：CE平分∠ACD.

答案： 证明:
∵∠BAC=∠ACE+∠E=∠ACE+β，∠BAC=α+2β，
∴∠ACE+β=α+2β，
∴∠ACE=α+β。
∵∠DCE=∠B+∠E=α+β，
∴∠ACE=∠DCE，
∴CE平分∠ACD。

14 推理能力 [2024太原期末]综合与实践
问题情境：数学课上,同学们以直角三角形为背景探究角之间的数量关系.
已知在Rt△ABC中,∠BAC = 90°,过点B作BM ⊥ BC,交△ABC的角平分线AD所在直线于点E. 设∠C的度数为α.
初步探究：
(1)如图1,当α ＜ 45°时,点E在线段DA的延长线上. “勤学”小组对这种情形进行了分析,提出如下问题,请你解答：
①当α = 25°时,求∠AEB的度数.
②用含α的式子表示∠AEB的度数：______.
拓展延伸：
(2)“智慧”小组借助图2进一步探究,当α ＞ 45°时,∠AEB与α之间的数量关系,请你补全图形并直接写出这个结论.

答案：

(1)①
∵∠BAC=∠CBE=90°，
∴∠C+∠ABC=∠ABC+∠ABE=90°，
∴∠ABE=∠C=25°。
∵AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$∠BAC=45°，
∴∠AEB=∠BAD−∠ABE=45°−25°=20°。②45°−α解法提示:
∵∠BAC=∠CBE=90°，
∴∠C+∠ABC=∠ABC+∠ABE=90°，
∴∠ABE=∠C=α。
∵AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$∠BAC=45°，
∴∠AEB=∠BAD−∠ABE=45°−α。
(2)补全的图形如图所示，∠AEB与α之间的数量关系为∠AEB=α−45°。 解法提示:
∵∠BAC=∠CBM=90°，
∴∠C+∠ABC=∠ABC+∠ABM=90°，
∴∠ABM=∠C=α。
∵AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$∠BAC=45°，
∴∠AEB=∠ABM−∠BAD=α−45°。