《2025年一遍过八年级数学上册人教版》

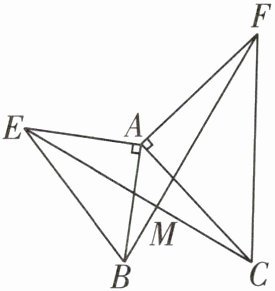
5 如图,在$\triangle ABE和\triangle ACF$中,$∠BAE= ∠CAF= 90^{\circ }$,$AE= AB$,$AC= AF$,EC与BF相交于点M。
(1)求证：$EC= BF$。
(2)求证：$EC⊥BF$。
(3)若$∠BAE= ∠CAF= m^{\circ }(m≠90)$,则(1)(2)中的结论还成立吗？请说明理由。

答案：

(1)证明：
∵∠BAE = ∠CAF = 90°，
∴∠BAE + ∠BAC = ∠CAF + ∠BAC，即∠EAC = ∠BAF。
在△CAE和△FAB中，
AE = AB，
∠EAC = ∠BAF，
AC = AF，
∴△CAE≌△FAB(SAS)，
∴EC = BF。
(2)证明：如图，设AC与BF交于点O。
由
(1)知△CAE≌△FAB，
∴∠AFO = ∠OCM，
∵∠AOF = ∠COM，
∴∠OMC = ∠OAF = 90°(在△AOF和△COM中，利用三角形内角和定理进行角度计算)，
∴EC⊥BF。

(3)解：
(1)中的结论成立，
(2)中的结论不成立。理由如下：
∵∠BAE = ∠CAF = m°，
∴∠BAE + ∠BAC = ∠CAF + ∠BAC，即∠EAC = ∠BAF。
在△CAE和△FAB中，
AE = AB，
∠EAC = ∠BAF，
AC = AF，
∴△CAE≌△FAB(SAS)，
∴EC = BF。
∴
(1)中的结论成立。
设AC与BF交于点N，由△CAE≌△FAB，得∠AFN = ∠MCN，
∵∠ANF = ∠CNM，
∴∠CMN = ∠NAF = m°，
∴
(2)中的结论不成立。

6 [2025惠州期中]已知D,A,E三点都在直线m上,点B,C在直线m同侧,且$AB= AC$。
(1)若$∠BDA= ∠AEC= ∠BAC$。
①如图1,若$AB⊥AC$,则BD与AE的数量关系为____,AD与CE的数量关系为____；
②如图2,猜想BD,CE与DE的数量关系并说明理由。
(2)如图3,若$∠BDA= ∠AEC$,$DE= 9cm$,$BD= 7cm$,点A在线段DE上以$2cm/s$的速度由点D向点E运动,同时,点C在线段EF上以$xcm/s$的速度由点E向点F运动,它们运动的时间为$t(s)$。是否存在x,使得$\triangle ABD与\triangle EAC$全等？若存在,求出相应的t值；若不存在,请说明理由。

答案： 解题思路：
(1)①利用平角的定义和三角形内角和定理得∠CAE = ∠ABD，再利用“AAS”证明△ABD≌△CAE，得BD = AE，AD = CE；②由
(1)①同理可得△ABD≌△CAE，得BD = AE，AD = CE，进而可得DE = BD + CE。
(2)分△DAB≌△ECA和△DAB≌△EAC两种情况讨论，再根据全等三角形的性质即可解决问题。
解：
(1)①BD = AE，AD = CE。
解法提示：
∵∠BDA = ∠AEC = ∠BAC，
∴∠BAD + ∠CAE = ∠BAD + ∠ABD，
∴∠CAE = ∠ABD。
又
∵∠BDA = ∠AEC，BA = AC，
∴△ABD≌△CAE(AAS)，
∴BD = AE，AD = CE。
②DE = BD + CE。理由如下：
由
(1)①同理可得△ABD≌△CAE，
∴BD = AE，AD = CE，
∴DE = AE + AD = BD + CE。
(2)存在。
当△DAB≌△ECA时，BD = AE，AD = CE。
∵BD = 7cm，DE = 9cm，
∴AE = 7cm，
∴CE = AD = 2cm，
∴t = 1，此时x = 2；
当△DAB≌△EAC时，AD = AE，BD = CE。
∵BD = 7cm，DE = 9cm，
∴AD = AE = $\frac{9}{2}$cm，DB = EC = 7cm，
∴t = $\frac{AD}{2}$ = $\frac{9}{4}$，此时x = 7÷$\frac{9}{4}$ = $\frac{28}{9}$。
综上，当x = 2时，t = 1；或当x = $\frac{28}{9}$时，t = $\frac{9}{4}$。