《2025年一遍过八年级数学上册人教版》

10 [2025河池期末]如图是一块三角形的草坪,现要在草坪上建一凉亭,要使凉亭到草坪三个顶点的距离相等,凉亭应选择的位置是( )


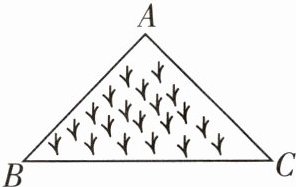
A.$ △ABC $三条中线的交点
B.$ △ABC $三条角平分线的交点
C.$ △ABC $三边的垂直平分线的交点
D.$ △ABC $三条高所在直线的交点

答案： C

11 下列说法中正确的是( )

A.任何一个命题都有逆命题
B.若原命题是假命题,则它的逆命题也是假命题
C.任何一个定理都有逆定理
D.若原命题是真命题,则它的逆命题也是真命题

答案： A

12 [2024定西安定区期中]如图,在$ △ABC $中,BD平分$ ∠ABC $,BC的垂直平分线交BC于点E,交BD于点F,连接CF,若$ ∠A = 60° $,$ ∠ABD = 20° $,则$ ∠ACF $的度数为( )

A.$ 30° $
B.$ 40° $
C.$ 50° $
D.$ 60° $

答案： D
∵BD平分∠ABC,∠ABD=20°,
∴∠CBD=∠ABD=20°,
∴∠ABC=40°.
∵EF垂直平分BC,
∴FB=FC,∠BEF=∠CEF=90°.在Rt△BEF和Rt△CEF中,{FB=FC,FE=FE,
∴Rt△BEF≌Rt△CEF(HL),
∴∠BCF=∠CBD=20°.在△ABC中,∠A=60°,
∴∠ACB=180° - ∠A - ∠ABC=80°,
∴∠ACF=∠ACB - ∠BCF=60°.

13 [2024天津南开区期中]如图,在$ △ABC $中,$ ∠BAC ＞ 90° $,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,连接AE,AF,若$ △AEF $的周长为7,则BC的长为____.

答案： 7
∵AB的垂直平分线交BC于点E,
∴EA=EB.
∵AC的垂直平分线交BC于点F,
∴FA=FC.
∵△AEF的周长为7,
∴BC=BE+EF+FC=AE+EF+AF=7.

14 易错题在$ △ABC $中,$ AB = AC $,O是平面内一点且$ OB = OC $,若点A到BC的距离为8,点O到BC的距离为4,则AO的长为____.

答案： 4或12
∵OB=OC,
∴点O在BC的垂直平分线上.
∵AB=AC,
∴点A在BC的垂直平分线上,
∴AO所在直线是BC的垂直平分线.分两种情况讨论:当点O与点A在BC的同侧时,AO=8 - 4=4;当点O与点A在BC的异侧时,AO=8+4=12.综上,AO的长为4或12.
名师点睛
本题由于点O的位置不明确,因此需要分点O与点A在BC的同侧和异侧两种情况求解.

15 推理能力[2025聊城阳谷期末]如图,$ AB = CD $,连接AC,BC,BD,线段AC的垂直平分线与线段BD的垂直平分线交于点E,连接BE,DE.若$ ∠CDE = 65° $,则$ ∠ABE $的度数为____.

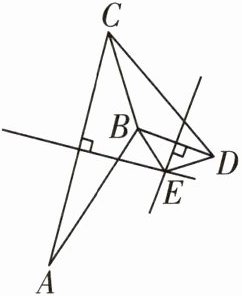
答案：
65° 如图,连接AE,CE,
∵AC,BD的垂直平分线相交于点E,
∴AE=CE,BE=DE.又
∵AB=CD,
∴△ABE≌△CDE,
∴∠ABE=∠CDE=65°.

16 推理能力|教材P93T10变式已知BD是$ △ABC $的角平分线.
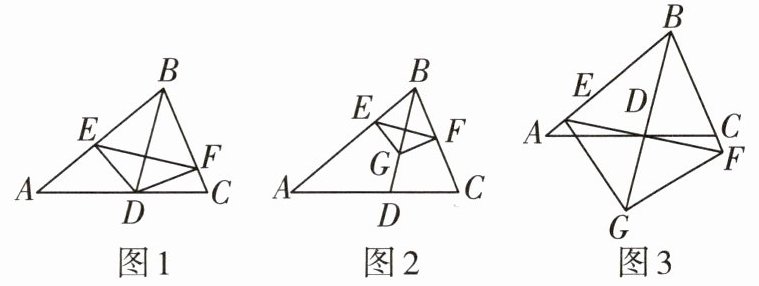
(1)如图1,$ DE ⊥ AB $于点E,$ DF ⊥ BC $于点F,连接EF.求证：BD所在直线是线段EF的垂直平分线.
(2)如图2,当线段BD上有一点G(不与点B重合)从点D向点B运动时,$ GE ⊥ AB $于点E,$ GF ⊥ BC $于点F,连接EF,此时(1)中的结论是否成立？请证明.
(3)如图3,当点G沿BD方向从点D沿BD的延长线运动时,$ GE ⊥ BA $(或其延长线)于点E,$ GF ⊥ BC $(或其延长线)于点F,连接EF,此时(1)中的结论是否成立？无需证明.

答案：
(1)证明:
∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DE=DF,
∴点D在线段EF的垂直平分线上.在Rt△BDE和Rt△BDF中,{DE=DF,BD=BD,
∴Rt△BDE≌Rt△BDF,
∴BE=BF,
∴点B在线段EF的垂直平分线上,
∴BD所在直线是线段EF的垂直平分线.
(2)解:成立.证明如下:同
(1)可证GE=GF,BE=BF,
∴点G,B在线段EF的垂直平分线上,
∴BG所在直线是线段EF的垂直平分线,即BD所在直线是线段EF的垂直平分线.
(3)解:成立.