第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 [2025杭州华东师大附中期中]
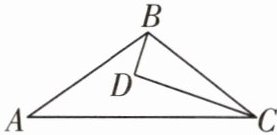
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A= ∠ABD,若BD= 1,BC= 3,则AC的长为 ( )
A.5
B.4
C.3
D.2

如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A= ∠ABD,若BD= 1,BC= 3,则AC的长为 ( )
A.5
B.4
C.3
D.2
答案:
1 A 如图,延长BD与AC交于点E(平分+垂直,延长构等腰).
∵∠A = ∠ABD,
∴BE = AE.
∵BD⊥CD,
∴BE⊥CD.
∵CD平分∠ACB,
∴∠BCD = ∠ECD,
∴∠EBC = ∠BEC,
∴BC = CE.
∵BE⊥CD,
∴2BD = BE;
∵BD = 1,BC = 3,
∴BE = 2,CE = 3,
∴AE = BE = 2,
∴AC = AE + EC = 2 + 3 = 5. 策略点拨等腰三角形的性质问题都可以利用三角形全等来解决,但要注意纠正不顾条件,一概依赖全等三角形的思维定势,凡可以直接利用等腰三角形的问题,应当优先选择简便方法来解决.
策略点拨等腰三角形的性质问题都可以利用三角形全等来解决,但要注意纠正不顾条件,一概依赖全等三角形的思维定势,凡可以直接利用等腰三角形的问题,应当优先选择简便方法来解决.
1 A 如图,延长BD与AC交于点E(平分+垂直,延长构等腰).
∵∠A = ∠ABD,
∴BE = AE.
∵BD⊥CD,
∴BE⊥CD.
∵CD平分∠ACB,
∴∠BCD = ∠ECD,
∴∠EBC = ∠BEC,
∴BC = CE.
∵BE⊥CD,
∴2BD = BE;
∵BD = 1,BC = 3,
∴BE = 2,CE = 3,
∴AE = BE = 2,
∴AC = AE + EC = 2 + 3 = 5.
 策略点拨等腰三角形的性质问题都可以利用三角形全等来解决,但要注意纠正不顾条件,一概依赖全等三角形的思维定势,凡可以直接利用等腰三角形的问题,应当优先选择简便方法来解决.
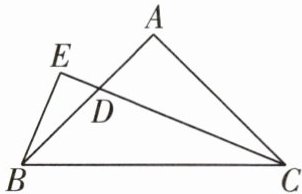
策略点拨等腰三角形的性质问题都可以利用三角形全等来解决,但要注意纠正不顾条件,一概依赖全等三角形的思维定势,凡可以直接利用等腰三角形的问题,应当优先选择简便方法来解决. 2 [2024呼和浩特期中]如图,在△ABC中,AB= AC,∠BAC= 90°,CD平分∠ACB,BE⊥CD交CD的延长线于点E.求证:CD= 2BE.

答案:
2 证明:如图,延长CA交BE的延长线于点F.
∵BE⊥CE,∠BAC = 90°,
∴∠BED = ∠CEF = ∠BAC = ∠BAF = 90°.
∵CD平分∠ACB,
∴∠1 = ∠2.在△CEF和△CEB中,∠1 = ∠2,CE = CE,∠CEF = ∠CEB,
∴△CEF≌△CEB(ASA),
∴EF = BE,
∴BF = 2BE.
∵∠4 = ∠5,
∴∠1 = ∠3(点拨:等角的余角相等).在△ACD和△ABF中,∠1 = ∠3,AC = AB,∠CAD = ∠BAF,
∴△ACD≌△ABF,
∴CD = BF,
∴CD = 2BE.
2 证明:如图,延长CA交BE的延长线于点F.
∵BE⊥CE,∠BAC = 90°,
∴∠BED = ∠CEF = ∠BAC = ∠BAF = 90°.
∵CD平分∠ACB,
∴∠1 = ∠2.在△CEF和△CEB中,∠1 = ∠2,CE = CE,∠CEF = ∠CEB,
∴△CEF≌△CEB(ASA),
∴EF = BE,
∴BF = 2BE.
∵∠4 = ∠5,
∴∠1 = ∠3(点拨:等角的余角相等).在△ACD和△ABF中,∠1 = ∠3,AC = AB,∠CAD = ∠BAF,
∴△ACD≌△ABF,
∴CD = BF,
∴CD = 2BE.

3 [2024池州贵池区期末]在等边三角形ABC中,点E在AB边上,点D在CB的延长线上,且ED= EC.
(1)【特殊情况,探索结论】
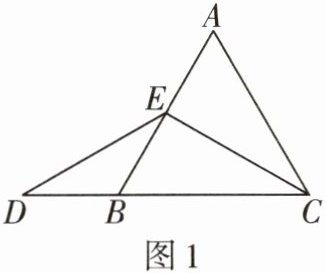
如图1,当E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AE____DB.(填“>”“<”或“=”)
(2)【特例启发,解答题目】
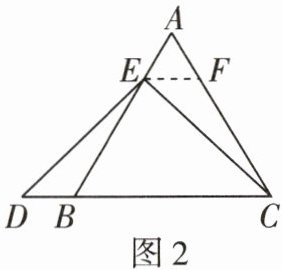
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE____DB(填“>”“<”或“=”),理由如下:
如图2,过点E作EF//BC,交AC于点F……(请你完成解答过程)
(3)【拓展结论,设计新题】
在等边三角形ABC中,点E在AB的延长线上,点D在CB的延长线上,且ED= EC,若△ABC的边长为1,AE= 2,求CD的长.(请你直接写出结果,并画出相应的图形)
(1)【特殊情况,探索结论】
如图1,当E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AE____DB.(填“>”“<”或“=”)
(2)【特例启发,解答题目】
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE____DB(填“>”“<”或“=”),理由如下:
如图2,过点E作EF//BC,交AC于点F……(请你完成解答过程)
(3)【拓展结论,设计新题】
在等边三角形ABC中,点E在AB的延长线上,点D在CB的延长线上,且ED= EC,若△ABC的边长为1,AE= 2,求CD的长.(请你直接写出结果,并画出相应的图形)


答案:
3 解:
(1)=
(2)=
理由如下:如题图2,过点E作EF//BC,交AC于点F,由△ABC为等边三角形,易知△AEF为等边三角形,可得AB = AC,AE = AF = EF,∠ABC = ∠ACB = 60°,
∴AB - AE = AC - AF,即BE = FC.
∵ED = EC,
∴∠D = ∠ECD,
∵∠DEB = ∠ABC - ∠D = 60° - ∠D,∠ECF = ∠ACB - ∠ECD = 60° - ∠ECD,
∴∠DEB = ∠ECF.在△DBE和△EFC中,DE = EC,∠DEB = ∠ECF,BE = FC,
∴△DBE≌△EFC(SAS),
∴DB = EF,
∴AE = DB.
(3)CD的长为3,图形如图所示.
解法提示:如图,当点E在AB的延长线上时,作EF//AC交CB的延长线于点F,则△EFB为等边三角形,同
(2)可证△DBE≌△CFE,
∴DB = FC,
∴DB - BF = FC - BF,即DF = BC.由AB = 1,AE = 2,易得BF = BE = 1,BC = AB = 1,
∴CD = DF + BF + BC = 3.
(1)=
(2)=
理由如下:如题图2,过点E作EF//BC,交AC于点F,由△ABC为等边三角形,易知△AEF为等边三角形,可得AB = AC,AE = AF = EF,∠ABC = ∠ACB = 60°,
∴AB - AE = AC - AF,即BE = FC.
∵ED = EC,
∴∠D = ∠ECD,
∵∠DEB = ∠ABC - ∠D = 60° - ∠D,∠ECF = ∠ACB - ∠ECD = 60° - ∠ECD,
∴∠DEB = ∠ECF.在△DBE和△EFC中,DE = EC,∠DEB = ∠ECF,BE = FC,
∴△DBE≌△EFC(SAS),
∴DB = EF,
∴AE = DB.
(3)CD的长为3,图形如图所示.
解法提示:如图,当点E在AB的延长线上时,作EF//AC交CB的延长线于点F,则△EFB为等边三角形,同
(2)可证△DBE≌△CFE,
∴DB = FC,
∴DB - BF = FC - BF,即DF = BC.由AB = 1,AE = 2,易得BF = BE = 1,BC = AB = 1,
∴CD = DF + BF + BC = 3.
查看更多完整答案,请扫码查看


