《2025年一遍过八年级数学上册人教版》

1 教材P129T1变式 下列各式中,能用平方差公式分解因式的是 ( )

A.$-x^{2}+9y^{2}$
B.$x^{2}+9y^{2}$
C.$x^{2}-2y^{2}+1$
D.$-x^{2}-9y^{2}$

答案： 1 A -x²+9y²是3y的平方与x的平方的差,能用平方差公式分解因式,故A选项符合题意.x²+9y²两项的符号相同,不能用平方差公式分解因式,故B选项不符合题意.x²-2y²+1是三项,不能用平方差公式分解因式,故C选项不符合题意.-x²-9y²两项的符号相同,不能用平方差公式分解因式,故D选项不符合题意.

2 [2023杭州中考]分解因式:$4a^{2}-1= $ ( )

A.$(2a-1)(2a+1)$
B.$(a-2)(a+2)$
C.$(a-4)(a+1)$
D.$(4a-1)(a+1)$

答案： 2 A 4a²-1=(2a)²-1²=(2a-1)(2a+1).

3 [2024德州中考]分解因式:$x^{2}-4= $____.

答案： 3 (x+2)(x-2) x²-4=x²-2²=(x+2)(x-2).

4 分解因式:$x^{2}-36y^{2}= $____.

答案： 4 (x+6y)(x-6y) x²-36y²=x²-(6y)²=(x+6y)(x-6y).

5 把$x^{2}-(y+1)^{2}$分解因式的结果是____.

答案： 5 (x+y+1)(x-y-1) x²-(y+1)²=[x+(y+1)][x-(y+1)]=(x+y+1)(x-y-1).

6 教材P129T2变式 分解因式:
(1)$16m^{2}-9n^{2}$;
(2)$x^{2}-\frac {1}{16}y^{2}$;
(3)$(a+1)^{2}-1$;
(4)$9(x+y)^{2}-(x-y)^{2}$.

答案： 6 解:
(1)16m²-9n²=(4m)²-(3n)²=(4m+3n)(4m-3n).
(2)x²-$\frac{1}{16}$y²=x²-($\frac{1}{4}$y)²=(x+$\frac{1}{4}$y)(x-$\frac{1}{4}$y).
(3)(a+1)²-1=(a+1+1)(a+1-1)=a(a+2).
(4)9(x+y)²-(x-y)²=[3(x+y)]²-(x-y)²=[3(x+y)+(x-y)][3(x+y)-(x-y)]=(3x+3y+x-y)(3x+3y-x+y)=(4x+2y)(2x+4y)=4(2x+y)(x+2y).

7 若$|x+y-6|+(x-y-3)^{2}= 0$,则$x^{2}-y^{2}= $____.

答案： 7 18 因为|x+y-6|≥0,(x-y-3)²≥0,所以x+y-6=0,x-y-3=0,所以x+y=6,x-y=3,所以x²-y²=(x+y)(x-y)=6×3=18.

8 用简便方法计算:$225^{2}-625$.

答案： 8 解:225²-625
=225²-25²
=(225+25)×(225-25)
=250×200
=50000.

9 小贤在抄题目时,不小心漏抄了二项式$a^{2}-□b^{2}$中“□”的部分,若该二项式能分解因式,则“□”不可能是 ( )

A.4
B.-9
C.25
D.16

答案： 9 B a²-4b²=(a-2b)(a+2b),故A选项不符合题意.a²+9b²不能分解因式,故B选项符合题意.a²-25b²=(a+5b)(a-5b),故C选项不符合题意;a²-16b²=(a+4b)(a-4b),故D选项不符合题意.

10 新趋势·代数推理 [2023河北中考]若k为任意整数,则$(2k+3)^{2}-4k^{2}$的值总能 ( )

A.被2整除
B.被3整除
C.被5整除
D.被7整除

答案： 10 B (2k+3)²-4k²=(2k+3)²-(2k)²=(2k+3+2k)(2k+3-2k)=3(4k+3).
∵3(4k+3)能被3整除,
∴(2k+3)²-4k²的值总能被3整除.

11 如图,从边长为$(a+3)$的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线剪开,拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的另一边长是____.

答案： 11 a+6 根据题意,得拼成的长方形的面积为(a+3)²-3²=(a+3+3)(a+3-3)=a(a+6).因为拼成的长方形的一边长为a,所以拼成的长方形的另一边长是a+6.

12 分解因式:$x^{2}-y^{2}+2x-2y= $____.

答案： 12 (x-y)(x+y+2) x²-y²+2x-2y=(x²-y²)+(2x-2y)=(x+y)(x-y)+2(x-y)=(x-y)(x+y+2).

13 应用意识 如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.
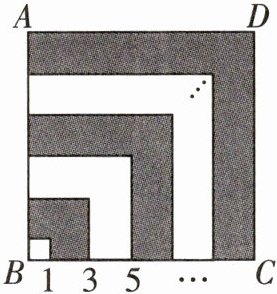
例如:$8= 3^{2}-1^{2},16= 5^{2}-3^{2},24= 7^{2}-5^{2}$,则8,16,24这三个数都是“奇特数”.
(1)填空:40____“奇特数”,2020____“奇特数”.(填“是”或“不是”)
(2)设两个连续奇数是$2n-1和2n+1$(其中n是正整数),由这两个连续奇数构造的“奇特数”是8的倍数吗? 为什么?
(3)如图,拼叠的正方形边长是从1开始的连续奇数,按此规律拼叠到正方形ABCD,其边长为199,求阴影部分的面积.

答案： 13 解:
(1)是 不是
(2)是.理由如下:
∵(2n+1)²-(2n-1)²
=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=8n,
∴由这两个连续奇数构造的“奇特数”是8的倍数.
(3)S阴影=199²-197²+195²-193²+…+7²-5²+3²-1²
=(199+197)(199-197)+(195+193)(195-193)+…+(7+5)(7-5)+(3+1)(3-1)
=(199+197+195+193+…+7+5+3+1)×2
=$\frac{(1+199)×100}{2}$×2
=20000.