第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 [2025 贵阳高坡民族中学期中]如图,在$\triangle ABC$中,$∠C= 90^{\circ },EF// AB,∠B= 39^{\circ }$,则$∠1$的度数为 ( )
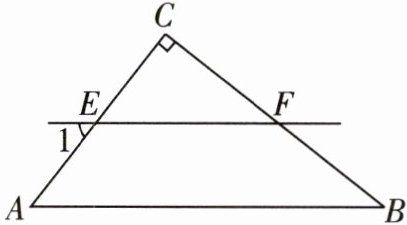
A.$39^{\circ }$
B.$51^{\circ }$
C.$38^{\circ }$
D.$52^{\circ }$

A.$39^{\circ }$
B.$51^{\circ }$
C.$38^{\circ }$
D.$52^{\circ }$
答案:
B 在△ABC中,∠C=90°,∠B=39°,
∴∠A=90°-∠B=51°.
∵EF//AB,
∴∠1=∠A=51°.
∴∠A=90°-∠B=51°.
∵EF//AB,
∴∠1=∠A=51°.
2 [一题多解[2025 抚顺望花区期中]在$Rt\triangle ABC$中,$∠C= 90^{\circ },∠A:∠B= 1:2$,则$∠A,∠B$的度数分别为 ( )
A.$30^{\circ }和60^{\circ }$
B.$45^{\circ }和45^{\circ }$
C.$40^{\circ }和80^{\circ }$
D.$60^{\circ }和30^{\circ }$
A.$30^{\circ }和60^{\circ }$
B.$45^{\circ }和45^{\circ }$
C.$40^{\circ }和80^{\circ }$
D.$60^{\circ }和30^{\circ }$
答案:
A 通解 由直角三角形的两锐角互余,得∠A+∠B=90°,
∵∠A:∠B=1:2,
∴∠A= $\frac{1}{1+2}$×90°=30°,∠B= $\frac{2}{1+2}$×90°=60°.
另解 由∠A:∠B=1:2,排除选项B,D,由三角形的内角和等于180°,排除选项C,故选项A符合题意.
∵∠A:∠B=1:2,
∴∠A= $\frac{1}{1+2}$×90°=30°,∠B= $\frac{2}{1+2}$×90°=60°.
另解 由∠A:∠B=1:2,排除选项B,D,由三角形的内角和等于180°,排除选项C,故选项A符合题意.
3 [教材 P14T1 变式[2025 昆明五华区期末]如图,在$\triangle ABC$中,$∠BAC= 90^{\circ },AC≠AB$,AD 是$\triangle ABC$的高,$DE⊥AC,DF⊥AB$,垂足分别为 E,F,则图中与$∠C$(∠C 除外)相等的角的个数是 ( )
A.3
B.4
C.5
D.6
A.3
B.4
C.5
D.6
答案:
A
∵∠BAC=90°,
∴∠C+∠B=90°,
∵AD是△ABC的高,DF⊥AB,
∴∠ADB=90°,∠BFD=90°,
∴∠BDF+∠B=90°,∠BAD+∠B=90°,
∴∠C=∠BDF=∠BAD.
∵AD是△ABC的高,DE⊥AC,
∴∠ADC=90°,∠AED=90°,
∴∠DAC+∠C=90°,∠DAC+∠ADE=90°,
∴∠C=∠ADE,
∴图中与∠C(∠C除外)相等的角的个数是3.
∵∠BAC=90°,
∴∠C+∠B=90°,
∵AD是△ABC的高,DF⊥AB,
∴∠ADB=90°,∠BFD=90°,
∴∠BDF+∠B=90°,∠BAD+∠B=90°,
∴∠C=∠BDF=∠BAD.
∵AD是△ABC的高,DE⊥AC,
∴∠ADC=90°,∠AED=90°,
∴∠DAC+∠C=90°,∠DAC+∠ADE=90°,
∴∠C=∠ADE,
∴图中与∠C(∠C除外)相等的角的个数是3.
4 [教材 P14 例 3 变式如图,在$Rt\triangle ABC$中,$∠C= 90^{\circ }$,AD 平分$∠CAB$交 BC 于点 D,$BE⊥AD$交AD 的延长线于点 E. 若$∠DBE= 25^{\circ }$,则$∠CAB$的度数为 _ .
答案:
50°
∵BE⊥AE,
∴∠E=90°,
∴∠DBE+∠BDE=90°.
∵∠C=90°,
∴∠CAD+∠CDA=90°.
∵∠BDE=∠CDA,
∴∠CAD=∠DBE=25°.
∵AD平分∠CAB,
∴∠CAB=2∠CAD=50°.
∵BE⊥AE,
∴∠E=90°,
∴∠DBE+∠BDE=90°.
∵∠C=90°,
∴∠CAD+∠CDA=90°.
∵∠BDE=∠CDA,
∴∠CAD=∠DBE=25°.
∵AD平分∠CAB,
∴∠CAB=2∠CAD=50°.
5 [2024 商丘睢阳区期末]如图,在$\triangle ABC$中,$∠ACB= 90^{\circ }$,将$\triangle ABC$沿 CD 折叠,使点 B 恰好落在 AC 边上的点 E 处. 若$∠A= 24^{\circ }$,则$∠EDC= $ _ $^{\circ }$.
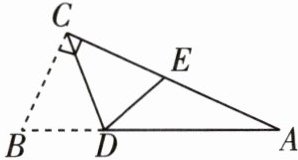

答案:
69 在△ABC中,∠ACB=90°,∠A=24°,
∴∠B=90°-∠A=66°.由折叠的性质,得∠CED=∠B=66°,∠ECD= $\frac{1}{2}$∠ACB=45°,
∴∠EDC=180°-∠ECD-∠CED=69°.
∴∠B=90°-∠A=66°.由折叠的性质,得∠CED=∠B=66°,∠ECD= $\frac{1}{2}$∠ACB=45°,
∴∠EDC=180°-∠ECD-∠CED=69°.
6 [2025 眉山东坡区期末]如图,在$\triangle ABC$中,$∠BAC= 90^{\circ },AD⊥BC$于点 D,BE 平分$∠ABC$交 AC 于点 E,AD,BE 相交于点 F.
(1)若$∠CAD= 36^{\circ }$,求$∠AEF$的度数.
(2)求证:$∠AEF= ∠AFE.$
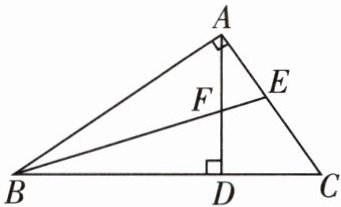
(1)若$∠CAD= 36^{\circ }$,求$∠AEF$的度数.
(2)求证:$∠AEF= ∠AFE.$

答案:
(1)解:
∵AD⊥BC,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°.
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABD=∠CAD=36°.
∵BE平分∠ABC,
∴∠ABE= $\frac{1}{2}$∠ABD=18°,
∴∠AEF=90°-∠ABE=72°.
(2)证明:
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠BAC=90°,∠ADB=90°,
∴∠ABE+∠AEF=90°,∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
∵∠AFE=∠BFD,
∴∠AEF=∠AFE.
∵AD⊥BC,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°.
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABD=∠CAD=36°.
∵BE平分∠ABC,
∴∠ABE= $\frac{1}{2}$∠ABD=18°,
∴∠AEF=90°-∠ABE=72°.
(2)证明:
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠BAC=90°,∠ADB=90°,
∴∠ABE+∠AEF=90°,∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
∵∠AFE=∠BFD,
∴∠AEF=∠AFE.
7 [教材 P14T2 变式如图,E 是$\triangle ABC$中 AC 边上的一点,过点 E 作$ED⊥AB$,垂足为点 D. 若$∠1= ∠2$,则$\triangle ABC$是 ( )
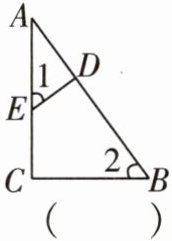
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定
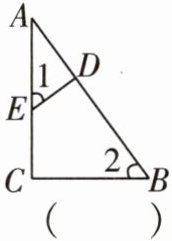
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定
答案:
A
∵ED⊥AB,
∴∠ADE=90°,
∴∠1+∠A=90°.
∵∠1=∠2,
∴∠2+∠A=90°,
∵∠C=90°,
∴△ABC是直角三角形.
∵ED⊥AB,
∴∠ADE=90°,
∴∠1+∠A=90°.
∵∠1=∠2,
∴∠2+∠A=90°,
∵∠C=90°,
∴△ABC是直角三角形.
8 [教材 P21T1 变式给出下列条件:①$∠A+∠B= ∠C$,②$∠A:∠B:∠C= 1:2:3$,③$∠A= 90^{\circ }-∠B$,④$∠A= ∠B= \frac {1}{2}∠C$,⑤$∠A= 2∠B= 3∠C$. 其中能确定$\triangle ABC$是直角三角形的有 ( )
A.2 个
B.3 个
C.4 个
D.5 个
A.2 个
B.3 个
C.4 个
D.5 个
答案:
C ①因为∠A+∠B=∠C,∠A+∠B+∠C=180°,所以2∠C=180°,所以∠C=90°,所以△ABC是直角三角形;②因为∠A:∠B:∠C=1:2:3,设∠A=x,则∠B=2x,∠C=3x,因为x+2x+3x=180°,所以x=30°,所以∠C=30°×3=90°,所以△ABC是直角三角形;③因为∠A=90°-∠B,所以∠A+∠B=90°,则∠C=180°-90°=90°,所以△ABC是直角三角形;④因为∠A=∠B= $\frac{1}{2}$∠C,所以∠A+∠B+∠C= $\frac{1}{2}$∠C+ $\frac{1}{2}$∠C+∠C=180°,所以∠C=90°,所以△ABC是直角三角形;⑤因为3∠C=2∠B=∠A,∠A+∠B+∠C=∠A+ $\frac{1}{2}$∠A+ $\frac{1}{3}$∠A=180°,所以∠A= $(\frac{1080}{11})$°,所以△ABC为钝角三角形.综上,能确定△ABC是直角三角形的有①②③④,共4个.
9 [2025 广安岳池期中]如图,在$\triangle ABC$中,AD 是 BC 边上的高,E 是 AB 边上一点,CE 交 AD 于点 M,且$∠DCM= ∠MAE$. 求证:$\triangle AEM$是直角三角形.
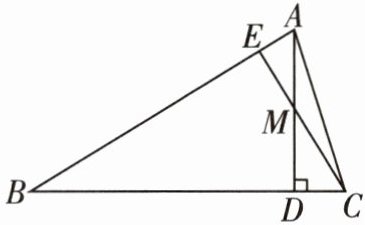

答案:
证明:
∵AD是BC边上的高,
∴AD⊥BC,
∴∠ADC=90°,
∴∠DMC+∠DCM=90°,
∵∠DMC=∠AME,∠DCM=∠MAE,
∴∠AME+∠MAE=90°,
∴∠AEM=90°,
∴△AEM是直角三角形.
∵AD是BC边上的高,
∴AD⊥BC,
∴∠ADC=90°,
∴∠DMC+∠DCM=90°,
∵∠DMC=∠AME,∠DCM=∠MAE,
∴∠AME+∠MAE=90°,
∴∠AEM=90°,
∴△AEM是直角三角形.
查看更多完整答案,请扫码查看


