《2025年暑假乐园海南出版社七年级数学华师大版》

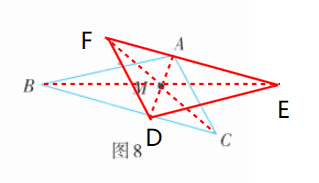
4. 如图8，画出△ABC关于点M成中心对称的△DEF，使得A，B，C的对应点分别为D，E，F。

答案：

5. 如图9，将△ABC沿EF折叠，使点C落在点C'处，试探究∠1、∠2与∠C的关系。

答案： 【解析】：
因为$\triangle EFC'$是由$\triangle EFC$折叠得到的，所以$\angle FEC=\angle FEC'$，$\angle EFC=\angle EFC'$。
$\angle 1 = 180^{\circ}-2\angle FEC$，$\angle 2 = 180^{\circ}-2\angle EFC$。
则$\angle 1+\angle 2 = 360^{\circ}-2(\angle FEC+\angle EFC)$。
在$\triangle EFC$中，$\angle FEC+\angle EFC = 180^{\circ}-\angle C$。
所以$\angle 1+\angle 2 = 360^{\circ}-2(180^{\circ}-\angle C)=2\angle C$。
【答案】：$\angle 1+\angle 2 = 2\angle C$