《2025年暑假乐园海南出版社七年级数学华师大版》

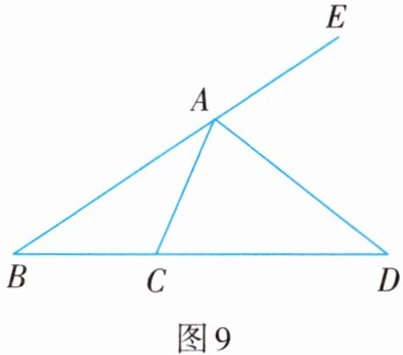
2. 如图9,在$\triangle ABC$中,$∠B=∠BAC,∠BAC$的外角平分线AD交BC的延长线于点D. 若$∠CAD=2∠ADC$,求$∠B$的度数.

答案： 【解析】：
设$\angle ADC = x$，因为$\angle CAD = 2\angle ADC$，所以$\angle CAD = 2x$。
因为$AD$平分$\angle CAE$，所以$\angle CAE = 2\angle CAD = 4x$。
因为$\angle BAC+\angle CAE = 180^{\circ}$，所以$\angle BAC = 180^{\circ}-4x$。
又因为$\angle B = \angle BAC$，所以$\angle B = 180^{\circ}-4x$。
因为$\angle B+\angle BAC+\angle ACB = 180^{\circ}$，且$\angle ACB=\angle CAD+\angle ADC = 3x$（三角形外角性质），所以$(180 - 4x)+(180 - 4x)+3x = 180$。
$\begin{aligned}180-4x + 180-4x+3x&=180\\360 - 5x&=180\\-5x&=180 - 360\\-5x&=-180\\x& = 36\end{aligned}$
则$\angle B=180^{\circ}-4x = 180 - 4\times36=36^{\circ}$。
【答案】：$36^{\circ}$