《2025年暑假乐园海南出版社七年级数学华师大版》

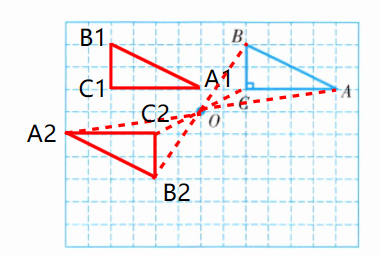
2. 如图6，在由边长为1个单位长度的小正方形组成的网格中，A，B，C都是格点。
（1）将△ABC向左平移6个单位长度得到△A₁B₁C₁，请画出△A₁B₁C₁；
（2）将△ABC绕点O按逆时针方向旋转180°得到△A₂B₂C₂，请画出△A₂B₂C₂。

答案：

3. 如图7，等边三角形ABC经过平移后得到△BDE，其平移的方向为点A到点B的方向，平移的距离为线段AB的长。△BDE能否看作是△ABC经过旋转得到的？如果能，请指出旋转中心，并说出旋转角度的大小。

答案： 【解析】：
因为$\triangle ABC$和$\triangle BDE$是等边三角形，所以$\angle ABC = \angle DBE = 60^{\circ}$。
那么$\angle CBE = 180^{\circ}-\angle ABC-\angle DBE = 180^{\circ}- 60^{\circ}-60^{\circ}=60^{\circ}$。
又因为$BC = BE$，所以$\triangle BDE$可以看作是$\triangle ABC$绕点$B$顺时针旋转$120^{\circ}$得到的（$\angle CBD = 120^{\circ}$）。
【答案】：
能，旋转中心是点$B$，旋转角度是$120^{\circ}$。