《2025年暑假乐园海南出版社七年级数学华师大版》

5. 如图2，$∠1$的度数为____。

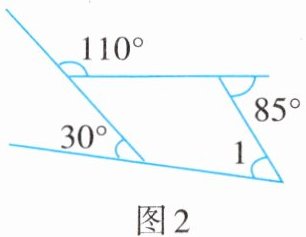
答案： $45^{\circ}$

6. 某公园的一段小路是由型号相同的五边形地砖平铺而成的，如图3所示，是平铺图案的一部分。如果每一个五边形中有三个内角相等，那么这三个内角的度数都等于____。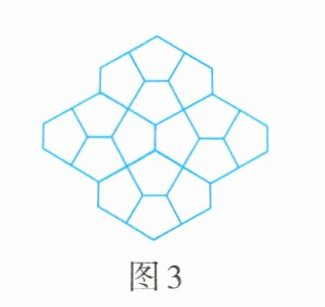

答案： $120^{\circ}$

7. 如果一个正多边形的内角和与外角和的比是$3:2$，那么这个正多边形是正____边形。

答案： 五

1. 一个多边形的每一个内角都等于$144^{\circ}$，求这个多边形的边数。

答案： 解：设这个多边形的边数为$n$。
根据多边形内角和公式$(n - 2)\times180^{\circ}$，已知每一个内角都等于$144^{\circ}$，则内角和为$144n^{\circ}$。
所以可得方程$(n - 2)\times180 = 144n$，
展开括号得$180n-360 = 144n$，
移项得$180n - 144n=360$，
即$36n = 360$，
解得$n = 10$。
所以这个多边形的边数是$10$。

2. 如果一个多边形外角和的5倍等于它的内角和，求这个多边形的边数。

答案： 【解析】：设这个多边形的边数为$n$。
多边形的外角和是$360^{\circ}$，内角和公式为$(n - 2)\times180^{\circ}$。
已知多边形外角和的$5$倍等于它的内角和，则可列方程：
$5\times360=(n - 2)\times180$
$1800 = 180n-360$
$180n=1800 + 360$
$180n=2160$
$n = 12$。
【答案】：$12$