第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
试一试,你一定很棒(十四)
今年,某市政府投入1000万元资金对城区4万户家庭的老式水龙头和13L抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
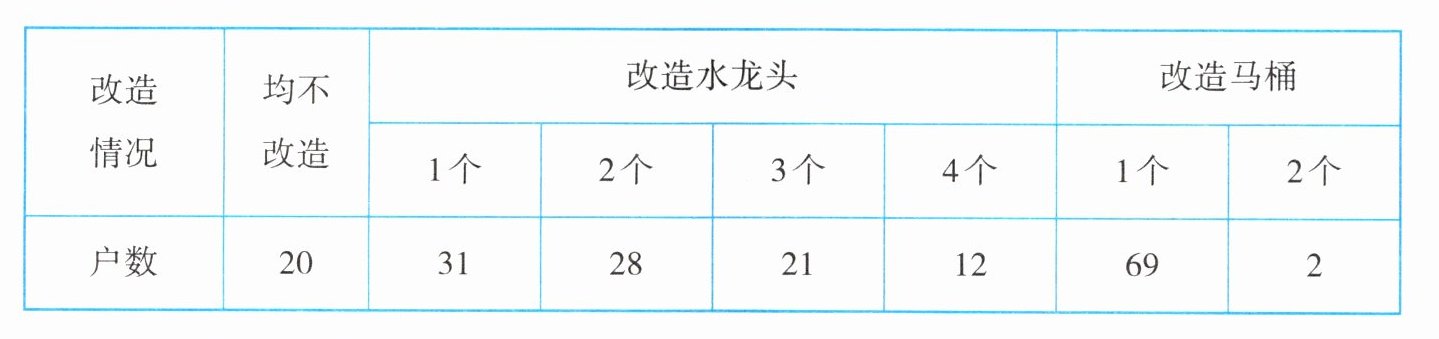
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有多少户.
(2)改造后,一个水龙头一年大约可节省5吨水,一个马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨水.
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
今年,某市政府投入1000万元资金对城区4万户家庭的老式水龙头和13L抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:

(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有多少户.
(2)改造后,一个水龙头一年大约可节省5吨水,一个马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨水.
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
答案:
【解析】:
(1) 首先计算抽样调查中需要对水龙头、马桶进行改造的家庭所占的比例,然后用该比例乘以社区的总户数,即可估计出该社区需要对水龙头、马桶进行改造的家庭户数。
在抽样的$120$户中,均不改造的有$20$户,则需要改造的有$120 - 20=100$户。
所以需要改造的家庭所占比例为$\frac{100}{120}=\frac{5}{6}$。
已知社区共有$1200$户家庭,则该社区需要对水龙头、马桶进行改造的家庭共有$1200\times\frac{5}{6}=1000$户。
(2) 分别计算抽样调查中改造水龙头和改造马桶一年节省的水量,进而求出抽样的$120$户家庭一年共节约的水量,再根据比例关系求出该社区一年共可节约的水量。
抽样的$120$户家庭中,改造水龙头的情况:
改造$1$个水龙头的有$31$户,改造$2$个水龙头的有$28$户,改造$3$个水龙头的有$21$户,改造$4$个水龙头的有$12$户,则改造水龙头的总数为:
$31\times1 + 28\times2+21\times3 + 12\times4$
$=31+56 + 63+48$
$=198$(个)
改造马桶的情况:改造$1$个马桶的有$69$户,改造$2$个马桶的有$2$户,则改造马桶的总数为:
$69\times1+2\times2=69 + 4 = 73$(个)
已知一个水龙头一年大约可节省$5$吨水,一个马桶一年大约可节省$15$吨水,则抽样的$120$户家庭一年共节约的水量为:
$198\times5+73\times15$
$=990+1095$
$=2085$(吨)
该社区共有$1200$户家庭,是抽样$120$户的$1200\div120 = 10$倍,所以该社区一年共可节约的水量为$2085\times10 = 20850$吨。
(3) 设既要改造水龙头又要改造马桶的家庭有$x$户。
改造水龙头的家庭有$31 + 28+21 + 12=92$户,改造马桶的家庭有$69 + 2=71$户,而需要改造的家庭有$100$户。
根据容斥原理:改造水龙头的户数$+$改造马桶的户数$-$既改造水龙头又改造马桶的户数$=$需要改造的户数,即$92+71 - x=100$,
$163 - x=100$,
解得$x = 63$户。
【答案】:
(1)$1000$户;
(2)$20850$吨;
(3)$63$户
(1) 首先计算抽样调查中需要对水龙头、马桶进行改造的家庭所占的比例,然后用该比例乘以社区的总户数,即可估计出该社区需要对水龙头、马桶进行改造的家庭户数。
在抽样的$120$户中,均不改造的有$20$户,则需要改造的有$120 - 20=100$户。
所以需要改造的家庭所占比例为$\frac{100}{120}=\frac{5}{6}$。
已知社区共有$1200$户家庭,则该社区需要对水龙头、马桶进行改造的家庭共有$1200\times\frac{5}{6}=1000$户。
(2) 分别计算抽样调查中改造水龙头和改造马桶一年节省的水量,进而求出抽样的$120$户家庭一年共节约的水量,再根据比例关系求出该社区一年共可节约的水量。
抽样的$120$户家庭中,改造水龙头的情况:
改造$1$个水龙头的有$31$户,改造$2$个水龙头的有$28$户,改造$3$个水龙头的有$21$户,改造$4$个水龙头的有$12$户,则改造水龙头的总数为:
$31\times1 + 28\times2+21\times3 + 12\times4$
$=31+56 + 63+48$
$=198$(个)
改造马桶的情况:改造$1$个马桶的有$69$户,改造$2$个马桶的有$2$户,则改造马桶的总数为:
$69\times1+2\times2=69 + 4 = 73$(个)
已知一个水龙头一年大约可节省$5$吨水,一个马桶一年大约可节省$15$吨水,则抽样的$120$户家庭一年共节约的水量为:
$198\times5+73\times15$
$=990+1095$
$=2085$(吨)
该社区共有$1200$户家庭,是抽样$120$户的$1200\div120 = 10$倍,所以该社区一年共可节约的水量为$2085\times10 = 20850$吨。
(3) 设既要改造水龙头又要改造马桶的家庭有$x$户。
改造水龙头的家庭有$31 + 28+21 + 12=92$户,改造马桶的家庭有$69 + 2=71$户,而需要改造的家庭有$100$户。
根据容斥原理:改造水龙头的户数$+$改造马桶的户数$-$既改造水龙头又改造马桶的户数$=$需要改造的户数,即$92+71 - x=100$,
$163 - x=100$,
解得$x = 63$户。
【答案】:
(1)$1000$户;
(2)$20850$吨;
(3)$63$户
查看更多完整答案,请扫码查看


