《2025年暑假乐园海南出版社七年级数学人教版》

8. 下列说法中，正确的是( )。
A. 不带根号的数不是无理数
B. 8的立方根是$\pm 2$
C. 绝对值是$\sqrt{3}$的实数是$\sqrt{3}$
D. 每个实数都对应数轴上的一个点

答案： D

9. 若$a^{2} = 4$，$|b| = 1$，则$a + b$的值为( )。
A. 3
B. $\pm 3$
C. $\pm 1$
D. $\pm 3$或$\pm 1$

答案： D

10. 已知$a^{3} = -27$，$\sqrt{b} = 2$，则$a + b$的平方根是( )。
A. 1
B. -1
C. $\pm 1$
D. -3或4

答案： C

2. 在2和3之间有______个有理数，______个无理数。

答案： 无数；无数

3. 面积为11的正方形边长为$x$，则$x$的整数部分是______。

答案： $3$

4. 若$\sqrt{m} = 1.3$，则$m =$______；若$\sqrt{y^{2}} = 6$，则$y =$______。

答案： $1.69$；$\pm6$

5. 一个自然数的算术平方根为$n$，则下一个自然数的平方根是______。

答案： $\pm\sqrt{n^{2}+1}$

6. 分别写出一个有理数和一个无理数，要求它们都是大于-2的负数：______。

答案： $-1$，$-\sqrt{2}$

7. 实数$a$在数轴上的位置如图3所示，化简$\sqrt{(a - 1)^{2}} + a$的结果是______。

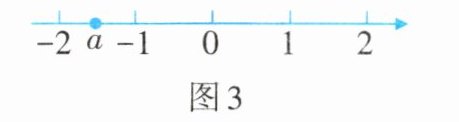
答案： 1

8. 若$\sqrt{12n}$是整数，则正整数$n$的最小值为______。

答案： $3$

1. 计算。
(1)$3\sqrt{5} - 2(\sqrt{5} + \sqrt{6})$；
(2)$\sqrt[3]{27} - \sqrt{9} + \sqrt{1 - (\frac{4}{5})^{2}}$；
(3)$\sqrt{(-3)^{2}} - (-\sqrt{3})^{2} - \sqrt{16} + \sqrt[3]{-64}$。

答案： 【解析】：
(1)
$\begin{aligned}&3\sqrt{5}-2(\sqrt{5}+\sqrt{6})\\=&3\sqrt{5}-2\sqrt{5}-2\sqrt{6}\\=&(3\sqrt{5}-2\sqrt{5}) - 2\sqrt{6}\\=&\sqrt{5}-2\sqrt{6}\end{aligned}$
(2)
$\begin{aligned}&\sqrt[3]{27}-\sqrt{9}+\sqrt{1 - (\frac{4}{5})^{2}}\\=&3 - 3+\sqrt{1-\frac{16}{25}}\\=&\sqrt{\frac{9}{25}}\\=&\frac{3}{5}\end{aligned}$
(3)
$\begin{aligned}&\sqrt{(-3)^{2}}-(-\sqrt{3})^{2}-\sqrt{16}+\sqrt[3]{-64}\\=&3 - 3-4+(-4)\\=&0-4 - 4\\=&-8\end{aligned}$
【答案】：
(1)$\sqrt{5}-2\sqrt{6}$；
(2)$\frac{3}{5}$；
(3)$-8$