《2025年暑假乐园海南出版社七年级数学人教版》

1. 在平面直角坐标系中描出下列各点,并用线段依次连接起来.观察得到的图形,你有何发现?
$(0,0),(1,1),(2,2),(3,3),(5,3),(5,2),(3,2),(3,0),(3,-2),(5,-2),(5,-3),(3,-3),(2,-2),(1,-1),(0,0)$.

答案： 【解析】：
1. 首先明确平面直角坐标系的概念：
在平面直角坐标系中，点的坐标$(x,y)$，$x$表示横坐标，$y$表示纵坐标。横坐标决定点在$x$轴上的位置，纵坐标决定点在$y$轴上的位置。
2. 然后依次描出各点：
对于点$(0,0)$，它是坐标原点，即$x$轴与$y$轴的交点。
点$(1,1)$，从原点出发，沿$x$轴正方向移动$1$个单位长度，再沿$y$轴正方向移动$1$个单位长度得到该点。
点$(2,2)$，从原点出发，沿$x$轴正方向移动$2$个单位长度，再沿$y$轴正方向移动$2$个单位长度得到该点。
点$(3,3)$，从原点出发，沿$x$轴正方向移动$3$个单位长度，再沿$y$轴正方向移动$3$个单位长度得到该点。
点$(5,3)$，从原点出发，沿$x$轴正方向移动$5$个单位长度，再沿$y$轴正方向移动$3$个单位长度得到该点。
点$(5,2)$，从原点出发，沿$x$轴正方向移动$5$个单位长度，再沿$y$轴正方向移动$2$个单位长度得到该点。
点$(3,2)$，从原点出发，沿$x$轴正方向移动$3$个单位长度，再沿$y$轴正方向移动$2$个单位长度得到该点。
点$(3,0)$，从原点出发，沿$x$轴正方向移动$3$个单位长度，$y$坐标为$0$，即在$x$轴上。
点$(3, - 2)$，从原点出发，沿$x$轴正方向移动$3$个单位长度，再沿$y$轴负方向移动$2$个单位长度得到该点。
点$(5,-2)$，从原点出发，沿$x$轴正方向移动$5$个单位长度，再沿$y$轴负方向移动$2$个单位长度得到该点。
点$(5,-3)$，从原点出发，沿$x$轴正方向移动$5$个单位长度，再沿$y$轴负方向移动$3$个单位长度得到该点。
点$(3,-3)$，从原点出发，沿$x$轴正方向移动$3$个单位长度，再沿$y$轴负方向移动$3$个单位长度得到该点。
点$(2,-2)$，从原点出发，沿$x$轴正方向移动$2$个单位长度，再沿$y$轴负方向移动$2$个单位长度得到该点。
点$(1,-1)$，从原点出发，沿$x$轴正方向移动$1$个单位长度，再沿$y$轴负方向移动$1$个单位长度得到该点。
最后回到点$(0,0)$。
3. 接着用线段依次连接各点：
连接后可以发现，图形关于原点对称，并且图形像一个“蝴蝶”形状。
【答案】：图形关于原点对称，像一个“蝴蝶”形状。

2. 如图5,在平面直角坐标系中,$△ABC$的顶点都在网格点上.其中,点$A$的坐标为$(2,-1)$,则$△ABC$的面积为多少?

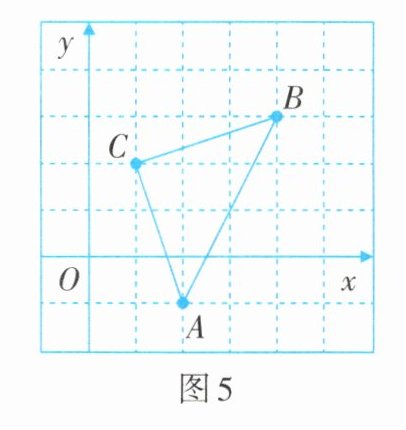
答案： $3×4-\frac{1}{2}×(1+3+1×3+2×4)=5$

3. 若点$P(2m+1,\frac {3m-1}{2})$在第四象限,求$m$的取值范围.

答案： 【解析】：因为点$P(2m + 1,\frac{3m - 1}{2})$在第四象限，根据第四象限内点的坐标特征：横坐标大于$0$，纵坐标小于$0$。
可得不等式组$\begin{cases}2m + 1\gt 0 \\ \frac{3m - 1}{2}\lt 0 \end{cases}$。
解不等式$2m+1\gt 0$，移项可得$2m\gt - 1$，两边同时除以$2$，解得$m\gt-\frac{1}{2}$。
解不等式$\frac{3m - 1}{2}\lt 0$，两边同时乘以$2$得$3m - 1\lt 0$，移项可得$3m\lt 1$，两边同时除以$3$，解得$m\lt\frac{1}{3}$。
所以$m$的取值范围是$-\frac{1}{2}\lt m\lt\frac{1}{3}$。
【答案】：$-\frac{1}{2}\lt m\lt\frac{1}{3}$