第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
1. 下列因式分解中正确的是(
A.$-a+a^{3}= -a(1+a^{2})$
B.$2a-4b+2= 2(a-2b)$
C.$a^{2}+4b^{2}= (a+2b)^{2}$
D.$a^{2}-2a+1= (a-1)^{2}$
D
)A.$-a+a^{3}= -a(1+a^{2})$
B.$2a-4b+2= 2(a-2b)$
C.$a^{2}+4b^{2}= (a+2b)^{2}$
D.$a^{2}-2a+1= (a-1)^{2}$
答案:
D
2. 下列命题中,是真命题的是(
A.三角形的一条角平分线将三角形的面积平分
B.同位角相等
C.如果$a^{2}= b^{2}$,那么$a= b$
D.$x^{2}-x+\frac {1}{4}$是完全平方式
D
)A.三角形的一条角平分线将三角形的面积平分
B.同位角相等
C.如果$a^{2}= b^{2}$,那么$a= b$
D.$x^{2}-x+\frac {1}{4}$是完全平方式
答案:
D
3. 若方程组$\left\{\begin{array}{l} 3x+y= k+1,\\ x+3y= 3\end{array} \right. 的解为\left\{\begin{array}{l} x= a,\\ y= b,\end{array} \right. 且a+b>0$,则k的取值范围是(
A.$k>4$
B.$k>-4$
C.$k<4$
D.$k<-4$
B
)A.$k>4$
B.$k>-4$
C.$k<4$
D.$k<-4$
答案:
B
4. 如图,在$\triangle ABC$中,点D在BC上,点O在AD上.如果$S_{\triangle AOB}= 3,S_{\triangle BOD}= 2,$$S_{\triangle ACO}= 1$,那么$S_{\triangle COD}$等于(
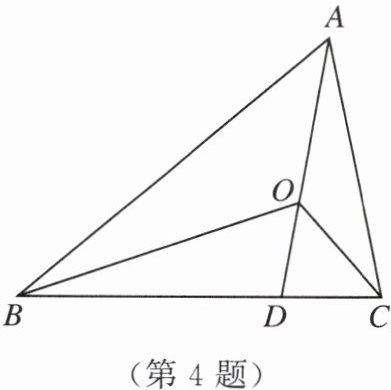
A.$\frac {1}{3}$
B.$\frac {1}{2}$
C.$\frac {3}{2}$
D.$\frac {2}{3}$
D
)
A.$\frac {1}{3}$
B.$\frac {1}{2}$
C.$\frac {3}{2}$
D.$\frac {2}{3}$
答案:
D
5. 命题“对顶角相等”的逆命题是____
假
____(填“真”或“假”)命题.
答案:
假
6. 若$a+b= 2$,则$a^{2}+ab+2b= $
4
.
答案:
4
7. 先化简,再求值:$(7m+n)^{2}-2(7m-n)$$(7m+n)+(7m-n)^{2}$,其中$m= 2025,$$n= -\frac {1}{2}.$
答案:
解:原式$=(7m+n)^{2}-2(7m-n)(7m+n)+(7m-n)^{2}$
$=[(7m+n)-(7m-n)]^{2}$
$=(7m+n-7m+n)^{2}$
$=(2n)^{2}$
$=4n^{2}$
当$n=-\frac{1}{2}$时,原式$=4×\left(-\frac{1}{2}\right)^{2}=4×\frac{1}{4}=1$
$=[(7m+n)-(7m-n)]^{2}$
$=(7m+n-7m+n)^{2}$
$=(2n)^{2}$
$=4n^{2}$
当$n=-\frac{1}{2}$时,原式$=4×\left(-\frac{1}{2}\right)^{2}=4×\frac{1}{4}=1$
8. 已知关于x,y的方程组 (m是常数).
(m是常数).
(1)若$x+y= 1$,求m的值;
(2)若$-5≤x-y≤2$,求m的取值范围;
(3)在(2)的条件下,化简:$|m+2|+$$|2m-3|.$
 (m是常数).
(m是常数).(1)若$x+y= 1$,求m的值;
(2)若$-5≤x-y≤2$,求m的取值范围;
(3)在(2)的条件下,化简:$|m+2|+$$|2m-3|.$
答案:
(1)解:①+②,得3x+3y=6m+1,
则x+y=2m+$\frac{1}{3}$,
∵x+y=1,
∴2m+$\frac{1}{3}$=1,
解得m=$\frac{1}{3}$;
(2)解:①-②,得x-y=2m-1,
∵-5≤x-y≤2,
∴-5≤2m-1≤2,
解得-2≤m≤$\frac{3}{2}$;
(3)解:
∵-2≤m≤$\frac{3}{2}$,
∴m+2≥0,2m-3≤0,
∴|m+2|+|2m-3|=m+2+3-2m=5-m.
(1)解:①+②,得3x+3y=6m+1,
则x+y=2m+$\frac{1}{3}$,
∵x+y=1,
∴2m+$\frac{1}{3}$=1,
解得m=$\frac{1}{3}$;
(2)解:①-②,得x-y=2m-1,
∵-5≤x-y≤2,
∴-5≤2m-1≤2,
解得-2≤m≤$\frac{3}{2}$;
(3)解:
∵-2≤m≤$\frac{3}{2}$,
∴m+2≥0,2m-3≤0,
∴|m+2|+|2m-3|=m+2+3-2m=5-m.
查看更多完整答案,请扫码查看


