第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
1. 下列运算中正确的是 (
A.$x^{3}+x^{2}= x^{5}$
B.$(3xy^{2})^{2}= 6x^{2}y^{4}$
C.$2x^{-1}= \frac {1}{2x}$
D.$(-x)^{7}÷(-x^{2})= x^{5}$
D
)A.$x^{3}+x^{2}= x^{5}$
B.$(3xy^{2})^{2}= 6x^{2}y^{4}$
C.$2x^{-1}= \frac {1}{2x}$
D.$(-x)^{7}÷(-x^{2})= x^{5}$
答案:
D
2. 将一张长方形纸片按如图所示的方式折叠,若$∠1= 40^{\circ }$,则$∠2$的度数是 (
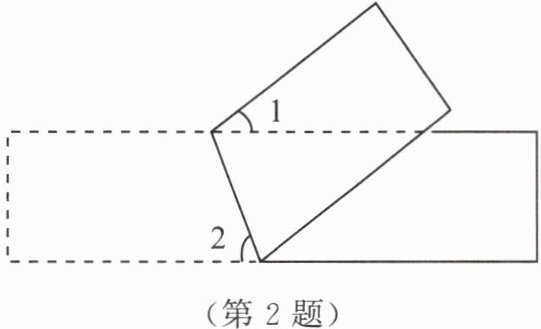
A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$70^{\circ }$
D
)
A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$70^{\circ }$
答案:
D
3. 若关于x,y的二元一次方程组$\left\{\begin{array}{l} 3x+y= a,\\ x-2y= 1\end{array} \right. 的解满足2x+3y= 2$,则a的值为 (
A.1
B.-3
C.3
D.4
C
)A.1
B.-3
C.3
D.4
答案:
C
4. 计算:$2a^{3}\cdot a^{4}=$
$2 a ^ { 7 }$
.
答案:
$2 a ^ { 7 }$
5. 若$m= 2n+1$,则$m^{2}-4mn+4n^{2}=$
1
.
答案:
1
6. 如图,在$△ABC$中,$∠A= ∠C,∠BDE= ∠BED$,BD平分$∠ABC$.若$∠CDE= 18^{\circ }$,则$∠A= $
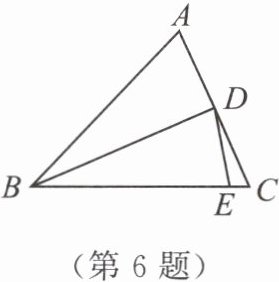
$54^{\circ }$
.
答案:
$54 ^ { \circ }$
7. 某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
|客车型号|A型号|B型号|
|载客量|45人/辆|30人/辆|
|租金|600元/辆|450元/辆|
(1)求A、B两种型号的客车各有多少辆.
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生去参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车;
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
|客车型号|A型号|B型号|
|载客量|45人/辆|30人/辆|
|租金|600元/辆|450元/辆|
(1)求A、B两种型号的客车各有多少辆.
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生去参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车;
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
答案:
$(1)$求$A$、$B$两种型号的客车各有多少辆
解:设$A$型号客车有$x$辆,$B$型号客车有$y$辆。
根据客车总数和载客量可列方程组$\begin{cases}x + y = 20\\45x + 30y = 720\end{cases}$
由$x + y = 20$可得$y = 20 - x$,将其代入$45x + 30y = 720$中:
$\begin{aligned}45x + 30(20 - x)&=720\\45x + 600 - 30x&=720\\15x&=720 - 600\\15x&=120\\x&=8\end{aligned}$
把$x = 8$代入$y = 20 - x$,得$y = 20 - 8 = 12$。
所以$A$型号客车有$8$辆,$B$型号客车有$12$辆。
$(2)$
①求最多能租用多少辆$A$型号客车
解:设租用$A$型号客车$m$辆,则租用$B$型号客车$(8 - m)$辆。
根据租车总费用不超过$4600$元,可列不等式$600m + 450(8 - m)\leq4600$
$\begin{aligned}600m + 3600 - 450m&\leq4600\\150m&\leq4600 - 3600\\150m&\leq1000\\m&\leq\frac{20}{3}\end{aligned}$
因为$m$为正整数,所以$m$的最大值为$6$。
即最多能租用$6$辆$A$型号客车。
②若七年级的师生共有$305$人,求租车方案
解:由师生人数可得不等式$45m + 30(8 - m)\geq305$
$\begin{aligned}45m + 240 - 30m&\geq305\\15m&\geq305 - 240\\15m&\geq65\\m&\geq\frac{13}{3}\end{aligned}$
又因为$m\leq\frac{20}{3}$且$m$为正整数,所以$m = 5$或$m = 6$。
当$m = 5$时,$8 - m = 8 - 5 = 3$,租车费用为$600×5 + 450×3 = 3000 + 1350 = 4350$(元)。
当$m = 6$时,$8 - m = 8 - 6 = 2$,租车费用为$600×6 + 450×2 = 3600 + 900 = 4500$(元)。
所以租车方案有两种:
方案一:租用$A$型号客车$5$辆,$B$型号客车$3$辆;
方案二:租用$A$型号客车$6$辆,$B$型号客车$2$辆。
因为$4350\lt4500$,所以最省钱的租车方案是租用$A$型号客车$5$辆,$B$型号客车$3$辆。
综上,答案依次为:$(1)$$\boldsymbol{A}$型号客车$\boldsymbol{8}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{12}$辆;$(2)$①$\boldsymbol{6}$辆;②租车方案有方案一:租用$\boldsymbol{A}$型号客车$\boldsymbol{5}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{3}$辆;方案二:租用$\boldsymbol{A}$型号客车$\boldsymbol{6}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{2}$辆。最省钱的租车方案是租用$\boldsymbol{A}$型号客车$\boldsymbol{5}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{3}$辆。
解:设$A$型号客车有$x$辆,$B$型号客车有$y$辆。
根据客车总数和载客量可列方程组$\begin{cases}x + y = 20\\45x + 30y = 720\end{cases}$
由$x + y = 20$可得$y = 20 - x$,将其代入$45x + 30y = 720$中:
$\begin{aligned}45x + 30(20 - x)&=720\\45x + 600 - 30x&=720\\15x&=720 - 600\\15x&=120\\x&=8\end{aligned}$
把$x = 8$代入$y = 20 - x$,得$y = 20 - 8 = 12$。
所以$A$型号客车有$8$辆,$B$型号客车有$12$辆。
$(2)$
①求最多能租用多少辆$A$型号客车
解:设租用$A$型号客车$m$辆,则租用$B$型号客车$(8 - m)$辆。
根据租车总费用不超过$4600$元,可列不等式$600m + 450(8 - m)\leq4600$
$\begin{aligned}600m + 3600 - 450m&\leq4600\\150m&\leq4600 - 3600\\150m&\leq1000\\m&\leq\frac{20}{3}\end{aligned}$
因为$m$为正整数,所以$m$的最大值为$6$。
即最多能租用$6$辆$A$型号客车。
②若七年级的师生共有$305$人,求租车方案
解:由师生人数可得不等式$45m + 30(8 - m)\geq305$
$\begin{aligned}45m + 240 - 30m&\geq305\\15m&\geq305 - 240\\15m&\geq65\\m&\geq\frac{13}{3}\end{aligned}$
又因为$m\leq\frac{20}{3}$且$m$为正整数,所以$m = 5$或$m = 6$。
当$m = 5$时,$8 - m = 8 - 5 = 3$,租车费用为$600×5 + 450×3 = 3000 + 1350 = 4350$(元)。
当$m = 6$时,$8 - m = 8 - 6 = 2$,租车费用为$600×6 + 450×2 = 3600 + 900 = 4500$(元)。
所以租车方案有两种:
方案一:租用$A$型号客车$5$辆,$B$型号客车$3$辆;
方案二:租用$A$型号客车$6$辆,$B$型号客车$2$辆。
因为$4350\lt4500$,所以最省钱的租车方案是租用$A$型号客车$5$辆,$B$型号客车$3$辆。
综上,答案依次为:$(1)$$\boldsymbol{A}$型号客车$\boldsymbol{8}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{12}$辆;$(2)$①$\boldsymbol{6}$辆;②租车方案有方案一:租用$\boldsymbol{A}$型号客车$\boldsymbol{5}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{3}$辆;方案二:租用$\boldsymbol{A}$型号客车$\boldsymbol{6}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{2}$辆。最省钱的租车方案是租用$\boldsymbol{A}$型号客车$\boldsymbol{5}$辆,$\boldsymbol{B}$型号客车$\boldsymbol{3}$辆。
查看更多完整答案,请扫码查看


