《2025年快乐过暑假江苏凤凰科学技术出版社七年级提升版》

1. 下面各组数据代表的三条线段长度,不能组成三角形的是 (D)
A.6 cm,9 cm,5 cm
B.6 cm,8 cm,10 cm
C.5 cm,7 cm,5 cm
D.12 cm,3 cm,7 cm

答案： D

2. 下列条件中,能判定△ABC为直角三角形的是 (D)
A.∠A = 2∠B - 3∠C
B.∠A + ∠B = 2∠C
C.∠A - ∠B = 30°
D.∠A = $\frac{1}{2}$∠B = $\frac{1}{3}$∠C

答案： D

3. 某校决定用1000元购买篮球和排球,其中篮球每个120元,排球每个80元,在购买资金恰好用尽的情况下,购买方案有 (A)
A.4种
B.3种
C.2种
D.1种

答案： A

4. 出水浮萍的果实质量只有0.000000076 g,用科学记数法表示是$7.6× 10^{-8}$g.

答案： $ 7.6 × 10 ^ { - 8 } $

5. 若代数式$x^{2}+3x+2可以表示为(x - 1)^{2}+a(x - 1)+b$的形式,则$a + b = $11.

答案： 11

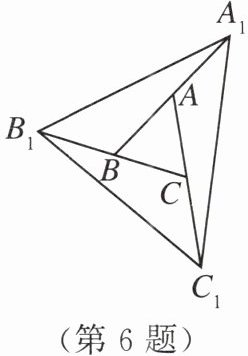
6. 如图,A,B,C分别是线段$A_{1}B$,$B_{1}C$,$C_{1}A$的中点,若△ABC的面积是2,则△$A_{1}B_{1}C_{1}$的面积是______14.

答案： 14

7. 如图,∠E = ∠1,∠3 + ∠ABC = 180°,BE是∠ABC的平分线.你能判断DF与AB的位置关系吗？请说明理由.

答案： $DF // AB$。理由如下：
∵ $BE$ 是 $\angle ABC$ 的平分线（已知），
∴ $\angle 1 = \angle 2$（角平分线的定义）。
∵ $\angle E = \angle 1$（已知），
∴ $\angle 2 = \angle E$（等量代换）。
∴ $AE // BC$（内错角相等，两直线平行）。
∴ $\angle ABC + \angle A = 180^\circ$（两直线平行，同旁内角互补）。
∵ $\angle 3 + \angle ABC = 180^\circ$（已知），
∴ $\angle 3 = \angle A$（同角的补角相等）。
∴ $DF // AB$（同位角相等，两直线平行）。

8. 如图,将△ABC经过一次平移后得到△$A'B'C'$,图中标出了点B的对应点$B'$.
(1)补全△$A'B'C'$；
(2)画出边AB上的中线CD；
(3)画出边BC上的高AE；
(4)求△$A'B'C'$的面积.(图中每个正方形小方格的边长为1)

答案：

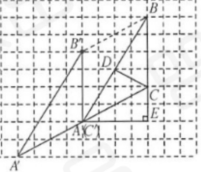
4. （4）
解：根据三角形面积公式$S = \frac{1}{2}ah$（$a$为底，$h$为高）。
对于$\triangle ABC$（平移前后三角形面积不变），以$BC$为底，$BC$的长度$a=\sqrt{(2)^{2}+(2)^{2}}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$（利用勾股定理$a=\sqrt{x^{2}+y^{2}}$，这里横向$x = 2$，纵向$y = 2$），通过数方格可知$BC$边上的高$h = 4$（利用方格的边长为$1$）。
也可以用割补法：$S_{\triangle ABC}=4×4-\frac{1}{2}×4×2-\frac{1}{2}×2×2-\frac{1}{2}×4×2$
$=16-(4 + 2+4)$
$=16 - 10$
$=6$。
因为$\triangle ABC$平移得到$\triangle A'B'C'$，根据平移的性质：平移不改变图形的形状和大小，所以$S_{\triangle A'B'C'}=S_{\triangle ABC}=6$。
综上，（1）、（2）、（3）按上述方法画图；（4）$\triangle A'B'C'$的面积为$6$。