《2025年优生ABC九年级数学上册人教版》

10. (2024·东莞市一模)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”，即利用圆的内接正多边形逼近圆的方法来近似估算，指出“割之弥细，所失弥少. 割之又割，以至于不可割，则与圆周合体，而无所失矣”. “割圆术”孕育了微积分思想，他用这种思想得到了圆周率π的近似值为3. 1416. 圆的半径为1，运用“割圆术”，以圆内接正十二边形面积近似估计圆的面积，可得π的估计值为3. 如图，若用半径为1的圆的内接正六边形面积作近似估计，可得π的估计值为 （B）

A. 3
B. 3√3/2
C. 2√3
D. 2√2

答案： B

11. (2024·广州市模拟)如图，正方形ABCD内接于⊙O，线段MN在对角线BD上运动，若⊙O的面积为2π，MN=1，则(1)⊙O的直径长为______2$\sqrt{2}$；(2)△AMN周长的最小值是______4.

答案：
(1)2$\sqrt{2}$　　
(2)4

12. (2024·广州市二模)如图，六边形ABCDEF是圆O的内接正六边形，设四边形ABCE的面积为S₁，△ACE的面积为S₂，则S₁/S₂=$\frac{4}{3}$.

答案： $\frac{4}{3}$

13. 如果一个矩形经过一个多边形的各顶点，那么我们把这个矩形叫作这个多边形的外接矩形. 如图，矩形ABCD是正六边形EFGHPQ的外接矩形，如果正六边形EFGHPQ的边长为2，那么矩形ABCD的长边与短边的比是 （A）

A. 2 : √3
B. 2 : √2
C. 3 : √3
D. √3 : 1

答案： A

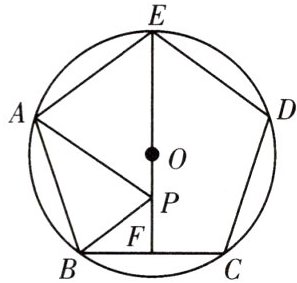
14. (一题多设问)如图，已知五边形ABCDE是⊙O的内接正五边形，过点E作EF⊥BC于点F，点P是线段EF上的动点，连接AP，BP.
(1)∠DEF的度数为______.
(2)求证：BF=CF.
(3)当点P与点O重合时，求S△BPF/S△ABP的值.
(4)当AP+BP的值最小时，求∠BPF的度数.

答案：
解：
(1)54°
(2)证明：如图，连接BE、CE.
　　　　　
由正五边形的定义，可得BA=AE=DE=CD，∠EAB=∠EDC，
∴△EAB≌△EDC.
∴EB=EC.
∵EF⊥BC，
∴BF=CF.
(3)由
(2)，得BF=CF.
∵EF⊥BC，
∴EF为BC的垂直平分线.
∴EF经过圆心O.
当点P与点O重合时，如图，过点O作OQ⊥AB于点Q.
　　　　　
∵OQ⊥AB，
∴AQ=BQ=$\frac{1}{2}$AB.
∵BF=FC=$\frac{1}{2}$BC，
∴AQ=BQ=BF.
∵AB=BC，OQ⊥AB，OF⊥BC，
∴由勾股定理，可得OQ=OF.
∴△OAQ，△OBQ，△OBF为等底等高的三角形.
∴S△OAQ=S△OBQ=S△OBF.
∴S△ABP=2S△OAQ，S△BPF=S△OAQ.
∴$\frac{S_{\triangle BPF}}{S_{\triangle ABP}}$=$\frac{1}{2}$.
(4)如图，连接AC，交EF于点P'，连接P'B，PC.
　　　　　
由
(3)，得EF为BC的垂直平分线，
∴PB=PC，P'B=P'C.
∴AP+BP=AP+PC，AC=AP'+P'C=AP'+P'B.
∵AP+PC≥AC，
∴AP+BP≥AP'+P'B.
∴当点P与点P'重合时，AP+BP的值最小.
∴∠BPF=∠BP'F.
∵AB=BC，∠ABC=108°，
∴∠ACB=∠BAC=36°.
∵EF⊥BC，P'B=P'C，
∴∠FP'C=∠FP'B=54°.
∴∠BPF的度数为54°.