《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

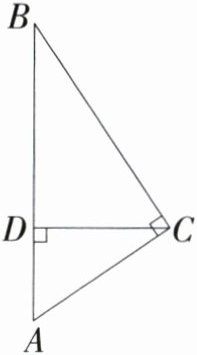
14.〔长春市〕如图,$\mathrm{Rt}\triangle ABC$中,$\angle ACB = 90^{\circ},CD\perp AB$于点$D$。
(1)求证：$AC^{2}=AB\cdot AD$；
(2)如果$BD = 5,AC = 6$，求$CD$的长。

答案： 解：
(1)证明：
∵CD⊥AB，
∴∠ADC = ∠ACB = 90°.
∵∠DAC = ∠CAB，
∴△ACD∽△ABC.
∴$\frac{AC}{AB}=\frac{AD}{AC}$.
∴$AC^2 = AB\cdot AD$.
(2)
∵$AC^2 = AB\cdot AD$，
∴$6^2=(AD + 5)\cdot AD$.
∵AD ＞ 0，
∴AD = 4.在Rt△ADC中，$CD=\sqrt{AC^2 - AD^2}=2\sqrt{5}$.

15.〔商水县〕问题发现
(1)如图1，已知正方形$ABCD$和正方形$AEFG$，写出$CF$与$DG$之间的数量关系：__________；
拓展探究
(2)将正方形$AEFG$绕点$A$顺时针旋转到图2所示的位置，连结$DG,CF$，试猜想$CF$与$DG$之间的数量关系，并说明理由；
类比迁移
(3)如图3，已知菱形$ABCD$和菱形$AEFG$，$\angle DAB = 60^{\circ}$，将菱形$AEFG$绕点$A$顺时针旋转$\alpha(0^{\circ}＜\alpha\leqslant60^{\circ})$，连结$DG,CF$，请在备用图中画出草图，判断$CF$与$DG$之间的数量关系是否随着$\alpha$的变化而变化，并说明理由。

答案：
解：
(1)$CF=\sqrt{2}DG$
(2)$CF=\sqrt{2}DG$.理由：连结AC，AF.
∵四边形ABCD和四边形AEFG为正方形，
∴∠DAC = ∠GAF = 45°，∠ADC = ∠AGF = 90°.
∴∠CAF = ∠DAG，$\frac{AC}{AD}=\frac{AF}{AG}=\sqrt{2}$.
∴△ACF∽△ADG.
∴$\frac{CF}{DG}=\frac{AF}{AG}=\sqrt{2}$，即$CF=\sqrt{2}DG$.
(3)如图所示.

CF与DG之间的数量关系不变.理由：连结AC，BD交于点O，连结AF.
∵四边形ABCD和四边形AEFG为菱形，
∴∠DAC = ∠GAF=$\frac{1}{2}$∠DAB = 30°，AC⊥BD，AO = CO.将菱形AEFG绕点A顺时针旋转α，则∠DAG = ∠CAF.在Rt△ADO中，
∵$\frac{AO}{AD}=\cos\angle DAC=\frac{\sqrt{3}}{2}$，
∴$\frac{AC}{AD}=\sqrt{3}$.同理，得$\frac{AF}{AG}=\sqrt{3}$.
∴$\frac{AC}{AD}=\frac{AF}{AG}=\sqrt{3}$.
∴△ACF∽△ADG.
∴$\frac{CF}{DG}=\frac{AF}{AG}=\sqrt{3}$，即$CF=\sqrt{3}DG$.
∴CF与DG之间的数量关系不变.