《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

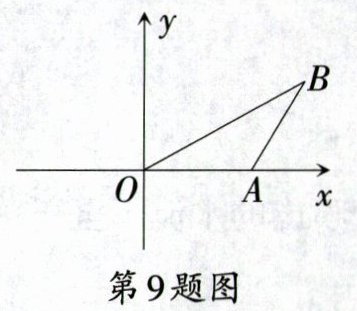
9. 如图，在平面直角坐标系中，已知点$A(2,0)$，$\angle OAB = 120^{\circ}$，$AB = AO$，且点$B$在第一象限内，将$\triangle OAB$绕点$O$顺时针旋转，每次旋转$60^{\circ}$，则第2024次旋转后点$B$的坐标是 ( )


A. $(3,-\sqrt{3})$
B. $(0,-2\sqrt{3})$
C. $(-3,-\sqrt{3})$
D. $(-3,\sqrt{3})$

答案： B 【解析】过点B作BH⊥x轴，垂足为H.
∵∠OAB = 120°，
∴∠BAH = 60°.
∵AB = AO，
∴∠AOB = ∠ABO = $\frac{1}{2}$∠BAH = 30°.
∵点A(2,0)，
∴AB = AO = 2. 在Rt△ABH中，
∵BH⊥x轴，
∴∠OHB = 90°.
∴∠ABH = 90° - ∠BAH = 30°.
∴AH = $\frac{1}{2}$AB = 1.
∴BH = $\sqrt{AB^{2}-AH^{2}}$ = $\sqrt{3}$.
∴OB = 2BH = 2$\sqrt{3}$.
∵将△OAB绕点O顺时针旋转，每次旋转60°，360°÷60° = 6，
∴每旋转6次为一个周期.
∵2024÷6 = 337……2，
∴第2024次旋转后，点B的位置与第2次旋转后相同.
∵60°×2 = 120°，60° + 120° = 180°，
∴△OAB绕点O顺时针旋转2次后，点B落在y轴负半轴上.
∴第2024次旋转后点B的坐标为(0,-2$\sqrt{3}$). 故选B.

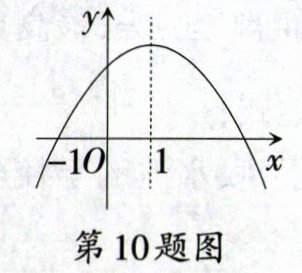
10. 如图是二次函数$y = ax^{2}+bx + c$的图象，其对称轴为直线$x = 1$. 下列结论：①$abc＞0$；②$2a + b = 0$；③$4a - 2b + c＜0$；④若$(-3,y_{1})$，$(4,y_{2})$是抛物线上两点，则$y_{1}＜y_{2}$. 其中结论正确的是 ( )


A. ①②
B. ①③④
C. ②④
D. ②③④

答案： D 【解析】
∵抛物线开口向下，对称轴为直线x = 1，与y轴交于正半轴，
∴a ＜ 0，-$\frac{b}{2a}$ = 1，c ＞ 0.
∴b = -2a ＞ 0.
∴2a + b = 0，abc ＜ 0. ①错误，②正确.
∵当x = -2时，y ＜ 0，
∴4a - 2b + c ＜ 0. ③正确.
∵抛物线的对称轴为直线x = 1，抛物线开口向下，且1 - (-3) ＞ 4 - 1，
∴y1 ＜ y2. ④正确. 综上所述，正确的结论是②③④. 故选D.

11. 杜牧在《清明》诗中写道“清明时节雨纷纷”，从数学的观点看，诗句中描述的事件是_______(选填“必然”或“随机”)事件.

答案： 随机

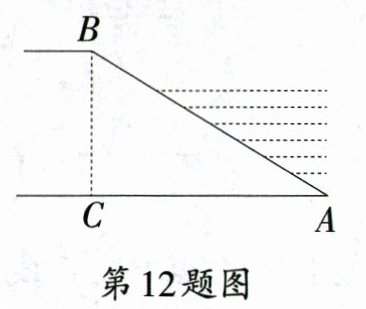
12. 如图，某河堤迎水坡$AB$的坡比$i = 1:\sqrt{6}$，河堤高$BC = 3\text{ m}$，则河堤的坡面$AB$的长为_______m.

答案： 3$\sqrt{7}$

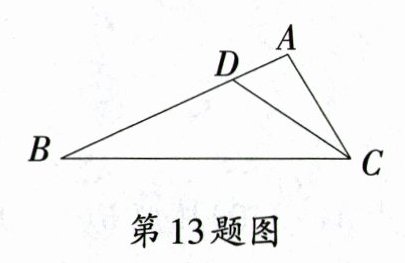
13. 如图，点$D$是$AB$边上的一点，若$\angle ACD=\angle B$，$AD = 1$，$AC = 2$，则$BD$的长为_______.

答案： 3

14. 已知$\triangle ABC$为等腰三角形，它的两条边的长度分别是方程$2x^{2}-7x + 5 = 0$的两个根，那么该三角形的周长是_______.

答案： 6 【解析】解方程2x² - 7x + 5 = 0，得x1 = $\frac{5}{2}$，x2 = 1.
分两种情况：①当等腰三角形的三边长为$\frac{5}{2}$，$\frac{5}{2}$，1时，符合三角形三边关系，此时等腰三角形的周长是$\frac{5}{2}$ + $\frac{5}{2}$ + 1 = 6. ②当等腰三角形的三边长为$\frac{5}{2}$，1，1时，1 + 1 ＜ $\frac{5}{2}$，不符合三角形三边关系，此时等腰三角形不存在. 综上所述，该等腰三角形的周长是6.

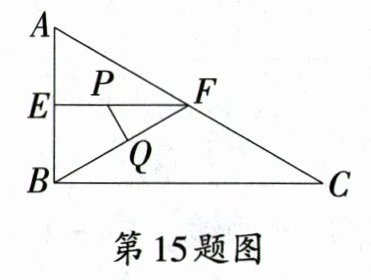
15. 如图，在$Rt\triangle ABC$中，$\angle ABC = 90^{\circ}$，$\angle ACB = 30^{\circ}$，$AB = 2\text{ cm}$，$E,F$分别是$AB,AC$的中点，动点$P$从点$E$出发，沿$EF$方向匀速运动，速度为$1\text{ cm/s}$，同时动点$Q$从点$B$出发，沿$BF$方向匀速运动，速度为$2\text{ cm/s}$，连结$PQ$. 设运动时间为$t\text{ s}(0＜t＜1)$，则当$t =$____________时，$\triangle PQF$为等腰三角形.

答案：
2 - $\sqrt{3}$或$\frac{6 + \sqrt{3}}{11}$ 【解析】
∵∠ABC = 90°，∠ACB = 30°，AB = 2 cm，
∴AC = 2AB = 4 cm.
∴BC = $\sqrt{AC^{2}-AB^{2}}$ = 2$\sqrt{3}$ cm.
∵E，F分别是AB，AC的中点，
∴EF = $\frac{1}{2}$BC = $\sqrt{3}$ cm，BF = $\frac{1}{2}$AC = 2 cm. 由题意得，EP = t cm，BQ = 2t cm.
∴PF = ($\sqrt{3}$ - t)cm，FQ = (2 - 2t) cm.
∴当△PQF为等腰三角形时，分三种情况：
①当PF = FQ时，如图①，则$\sqrt{3}$ - t = 2 - 2t，
∴t = 2 - $\sqrt{3}$.
②当PQ = FQ时，如图②，过点Q作QD⊥EF于点D.
∴PF = 2DF.
∵BF = CF，
∴∠FBC = ∠C = 30°.
∵E，F分别是AB，AC的中点，
∴EF//BC.
∴∠PFQ = ∠FBC = 30°.
∵FQ = (2 - 2t) cm，
∴DQ = $\frac{1}{2}$FQ = (1 - t) cm.
∴DF = $\sqrt{3}$(1 - t)cm.
∴PF = 2DF = 2$\sqrt{3}$(1 - t)cm.
∴2$\sqrt{3}$(1 - t) = $\sqrt{3}$ - t.
∴t = $\frac{6 + \sqrt{3}}{11}$.
③当PF = PQ时，∠PFQ = ∠PQF = 30°.
∴∠FPQ = 120°.
在P，Q运动过程中，∠FPQ小于90°，此种情况不成立.
综上所述，当t = 2 - $\sqrt{3}$或t = $\frac{6 + \sqrt{3}}{11}$时，△PQF为等腰三角形.
　

三、解答题（共8小题，共75分）
16. （8分）计算：$(x^{2}+\sqrt{2})^{0}+\sqrt{\frac{1}{8}}\times(\frac{1}{2})^{-1}-\vert1-\cos45^{\circ}\vert$.

答案： 解：原式 = 1 + $\frac{\sqrt{2}}{4}$×2 - 1 + $\frac{\sqrt{2}}{2}$ （5分）
= $\sqrt{2}$. （8分）