2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 不透明的盒子里装有除所标数字外完全相同的三个小球,球上分别标有数字-2,1,4,随机摸出一个小球,其数字记为p,放回,再随机摸出一个小球,其数字记为q,则满足关于x的方程$x^{2}+px + q = 0$有实数根的概率是 ( )
A. $\frac{1}{9}$
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{8}{9}$
A. $\frac{1}{9}$
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{8}{9}$
答案:
C [解析]根据题意,画树状图表示出所有可能出现的结果如下.

由树状图可知,共有9种等可能的结果,其中满足关于x的方程$x^{2}+px + q = 0$有实数根(即$p^{2}-4q\geq0$)的结果有6种.
∴P(满足关于x的方程$x^{2}+px + q = 0$有实数根)=$\frac{6}{9}$=$\frac{2}{3}$.故选C.
C [解析]根据题意,画树状图表示出所有可能出现的结果如下.

由树状图可知,共有9种等可能的结果,其中满足关于x的方程$x^{2}+px + q = 0$有实数根(即$p^{2}-4q\geq0$)的结果有6种.
∴P(满足关于x的方程$x^{2}+px + q = 0$有实数根)=$\frac{6}{9}$=$\frac{2}{3}$.故选C.
8. 〔跨学科 物理〕如图所示的电路图中,随机闭合开关$S_{1}$,$S_{2}$,$S_{3}$中的两个,则能让两盏灯泡同时发光的概率为 ( )

A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{6}$
D. $\frac{2}{3}$

A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{6}$
D. $\frac{2}{3}$
答案:
D
9.〔烟台模拟〕一张圆桌旁设有4个座位,丙先坐在了如图所示的座位上,甲、乙两人等可能地坐到①,②,③中的2个座位上. 乙坐在②号座位的概率为$P_{1}$,甲与乙不是相邻而坐的概率为$P_{2}$,则下列结论正确的是 ( )
A. $P_{1}=P_{2}$
B. $2P_{1}=P_{2}$
C. $P_{1}>P_{2}$
D. $P_{1}+P_{2}=1$

A. $P_{1}=P_{2}$
B. $2P_{1}=P_{2}$
C. $P_{1}>P_{2}$
D. $P_{1}+P_{2}=1$
答案:
A [解析]根据题意,画树状图表示出所有可能出现的结果如下:
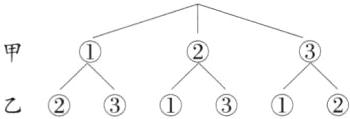
由树状图可知,共有6种等可能的结果.其中乙坐在②号座位的结果有2种,甲与乙不是相邻而坐的结果有2种.
∴乙坐在②号座位的概率$P_{1}=\frac{2}{6}$=$\frac{1}{3}$,甲与乙不是相邻而坐的概率$P_{2}=\frac{2}{6}$=$\frac{1}{3}$
∴$P_{1}=P_{2}$.故选A.
A [解析]根据题意,画树状图表示出所有可能出现的结果如下:

由树状图可知,共有6种等可能的结果.其中乙坐在②号座位的结果有2种,甲与乙不是相邻而坐的结果有2种.
∴乙坐在②号座位的概率$P_{1}=\frac{2}{6}$=$\frac{1}{3}$,甲与乙不是相邻而坐的概率$P_{2}=\frac{2}{6}$=$\frac{1}{3}$
∴$P_{1}=P_{2}$.故选A.
10.〔沈阳模拟〕从1,3,5三个数中选取一个数作为x的值,使二次根式$\sqrt{6 - 2x}$有意义的概率为_______.
答案:
$\frac{2}{3}$
11.〔昆明市〕“头盔是生命之盔”,质检部门对某工厂生产的头盔进行质量抽查,抽查结果如表:
|抽查的头盔数n|100|200|300|500|800|1 000|3 000|
|----|----|----|----|----|----|----|----|
|合格的头盔数m|95|191|289|479|769|960|2 880|
|合格头盔的频率$\frac{m}{n}$(精确到0.001)|0.950|0.955|0.963|0.958|0.961|0.960|0.960|
如果从该工厂生产出来的头盔中任取一个,那么该头盔合格的概率为_______.(精确到0.01)
|抽查的头盔数n|100|200|300|500|800|1 000|3 000|
|----|----|----|----|----|----|----|----|
|合格的头盔数m|95|191|289|479|769|960|2 880|
|合格头盔的频率$\frac{m}{n}$(精确到0.001)|0.950|0.955|0.963|0.958|0.961|0.960|0.960|
如果从该工厂生产出来的头盔中任取一个,那么该头盔合格的概率为_______.(精确到0.01)
答案:
0.96
12. 如图,已知等边三角形ABC的面积为1,D,E分别为AB,AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是_______.(不考虑落在线上的情形)


答案:
$\frac{3}{4}$
13.〔朝霞原创〕一枚质地均匀的骰子六个面上分别刻有1到6的点数,掷两次骰子,得到向上一面的点数分别为m,n,则点A(m,n)在正比例函数$y = 2x$的图象上的概率是_______.
答案:
$\frac{1}{12}$ [解析]根据题意可列表表示出所有可能出现的结果如下:
1 2 3 4 5 6
1 (1,1)(2,1)(3,1)(4,1)(5,1)(6,1)
2 (1,2)(2,2)(3,2)(4,2)(5,2)(6,2)
3 (1,3)(2,3)(3,3)(4,3)(5,3)(6,3)
4 (1,4)(2,4)(3,4)(4,4)(5,4)(6,4)
5 (1,5)(2,5)(3,5)(4,5)(5,5)(6,5)
6 (1,6)(2,6)(3,6)(4,6)(5,6)(6,6)
由上表可得共有36种等可能的结果,其中点$A(m,n)$在正比例函数$y = 2x$图象上的点有$(1,2)$,$(2,4)$,$(3,6)$,共3种.
∴P(点A在正比例函数$y = 2x$的图象上)=$\frac{3}{36}$=$\frac{1}{12}$.
1 2 3 4 5 6
1 (1,1)(2,1)(3,1)(4,1)(5,1)(6,1)
2 (1,2)(2,2)(3,2)(4,2)(5,2)(6,2)
3 (1,3)(2,3)(3,3)(4,3)(5,3)(6,3)
4 (1,4)(2,4)(3,4)(4,4)(5,4)(6,4)
5 (1,5)(2,5)(3,5)(4,5)(5,5)(6,5)
6 (1,6)(2,6)(3,6)(4,6)(5,6)(6,6)
由上表可得共有36种等可能的结果,其中点$A(m,n)$在正比例函数$y = 2x$图象上的点有$(1,2)$,$(2,4)$,$(3,6)$,共3种.
∴P(点A在正比例函数$y = 2x$的图象上)=$\frac{3}{36}$=$\frac{1}{12}$.
14.〔南阳市〕一个不透明的口袋中装有四个形状、大小、质地都相同的小球,把它们分别标号为1,2,3,4.
(1)随机摸取一个小球,其标号是“3”,该事件的概率为_______.
(2)随机摸取一个小球记下标号后放回,搅匀后从中再随机摸取一个小球,记下标号. 用列表或画树状图的方法求取出的2个小球中,至少有1个的标号为“3”的概率.
(3)若小东和小明先后随机摸取一个小球(取走后不放回),请直接写出小东和小明取走的小球标号都不为“3”的概率.
(1)随机摸取一个小球,其标号是“3”,该事件的概率为_______.
(2)随机摸取一个小球记下标号后放回,搅匀后从中再随机摸取一个小球,记下标号. 用列表或画树状图的方法求取出的2个小球中,至少有1个的标号为“3”的概率.
(3)若小东和小明先后随机摸取一个小球(取走后不放回),请直接写出小东和小明取走的小球标号都不为“3”的概率.
答案:
解:
(1)$\frac{1}{4}$
(2)根据题意,画树状图表示出所有可能出现的结果如下.

由图可知,共有16种等可能的结果,取出的2个小球中,至少有1个的标号为“3”的结果有7种.
∴P(取出的2个小球中,至少有1个的标号为“3”)=$\frac{7}{16}$.
(3)小东和小明取走的小球标号都不为“3”的概率为$\frac{1}{2}$.
解:
(1)$\frac{1}{4}$
(2)根据题意,画树状图表示出所有可能出现的结果如下.

由图可知,共有16种等可能的结果,取出的2个小球中,至少有1个的标号为“3”的结果有7种.
∴P(取出的2个小球中,至少有1个的标号为“3”)=$\frac{7}{16}$.
(3)小东和小明取走的小球标号都不为“3”的概率为$\frac{1}{2}$.
15. 某校在开展“网络安全知识教育周”期间,从九年级随机抽取了20名学生分成甲、乙两组,每组各10人,进行“网络安全”现场知识竞赛. 把甲、乙两组的成绩进行整理分析(满分100分,竞赛得分用x表示,单位:分),$90\leq x\leq100$为网络安全意识非常强,$80\leq x<90$为网络安全意识强,$x<80$为网络安全意识一般.
收集整理的数据制成如下两幅统计图:
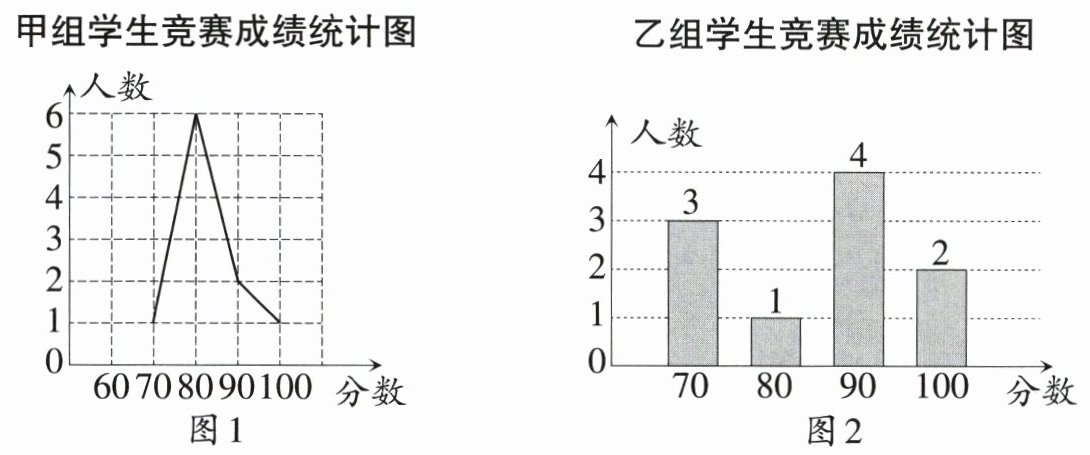
分析数据:
| |平均数|中位数|众数|方差|
|----|----|----|----|----|
|甲组|83|80|c|61|
|乙组|a|b|90|125|
根据以上信息回答下列问题:
(1)填空:a = _______,b = _______,c = _______.
(2)你认为哪个组的成绩更好?请说明理由.
(3)现在准备从甲、乙两组满分的同学中抽取两名同学参加校级比赛,求抽取的两名同学恰好一人来自甲组,另一人来自乙组的概率.
收集整理的数据制成如下两幅统计图:

分析数据:
| |平均数|中位数|众数|方差|
|----|----|----|----|----|
|甲组|83|80|c|61|
|乙组|a|b|90|125|
根据以上信息回答下列问题:
(1)填空:a = _______,b = _______,c = _______.
(2)你认为哪个组的成绩更好?请说明理由.
(3)现在准备从甲、乙两组满分的同学中抽取两名同学参加校级比赛,求抽取的两名同学恰好一人来自甲组,另一人来自乙组的概率.
答案:
解:
(1)85 90 80
(2)乙组的成绩更好.理由:乙组成绩的平均数、中位数、众数均高于甲组,所以乙组的成绩更好.(答案合理即可)
(3)记乙组2名满分的同学分别为乙$_{1}$、乙$_{2}$,抽取的两名同学为第1人、第2人.列表表示出所有可能出现的结果如下.
第2人 第1人 甲 乙$_{1}$ 乙$_{2}$
甲 (乙$_{1}$,甲)(乙$_{2}$,甲)
乙$_{1}$ (甲,乙$_{1}$) (乙$_{2}$,乙$_{1}$)
乙$_{2}$ (甲,乙$_{2}$)(乙$_{1}$,乙$_{2}$)
由表可知,共有6种等可能出现的结果,其中两名同学恰好一人来自甲组,另一人来自乙组的结果有4种.
∴P(两名同学恰好一人来自甲组,另一人来自乙组)=$\frac{4}{6}$=$\frac{2}{3}$.
(1)85 90 80
(2)乙组的成绩更好.理由:乙组成绩的平均数、中位数、众数均高于甲组,所以乙组的成绩更好.(答案合理即可)
(3)记乙组2名满分的同学分别为乙$_{1}$、乙$_{2}$,抽取的两名同学为第1人、第2人.列表表示出所有可能出现的结果如下.
第2人 第1人 甲 乙$_{1}$ 乙$_{2}$
甲 (乙$_{1}$,甲)(乙$_{2}$,甲)
乙$_{1}$ (甲,乙$_{1}$) (乙$_{2}$,乙$_{1}$)
乙$_{2}$ (甲,乙$_{2}$)(乙$_{1}$,乙$_{2}$)
由表可知,共有6种等可能出现的结果,其中两名同学恰好一人来自甲组,另一人来自乙组的结果有4种.
∴P(两名同学恰好一人来自甲组,另一人来自乙组)=$\frac{4}{6}$=$\frac{2}{3}$.
查看更多完整答案,请扫码查看


