《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

8. 如图,已知AB是⊙O的直径,DA与⊙O相切于点A,$\widehat{EC}=\widehat{CB}$,则下列结论中不一定正确的是 ( )


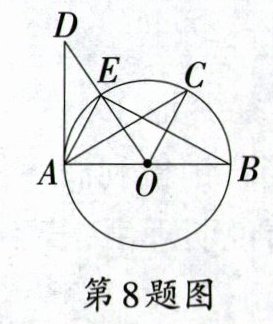
A. $BA\perp DA$
B. $OC// AE$
C. $\angle COE = 2\angle EAC$
D. $OD\perp AC$

答案： D

9. 已知抛物线$y = x^{2}+bx + c$的部分图象如图所示，以下结论：①$abc＞0$；②方程$x^{2}+bx + c = 0$的根是$x_{1}=-1$，$x_{2}=3$；③抛物线上有三点$(-1,y_{1})$，$(1,y_{2})$，$(4,y_{3})$，则$y_{1}＞y_{3}＞y_{2}$；④若$-1＜x＜2$，则y的取值范围是$-4\leq y＜0$。其中正确的有 ( )


A. ①②
B. ①②③
C. ①②④
D. ①②③④

答案： C

10. 如图，在矩形ABCD中，AB = 1，BC = 2，连结AC，以对角线AC为边，按逆时针方向作矩形$ACC_{1}B_{1}$，使矩形$ACC_{1}B_{1}\sim$矩形ADCB；再连结$AC_{1}$，以对角线$AC_{1}$为边，按逆时针方向作矩形$AC_{1}C_{2}B_{2}$，使矩形$AC_{1}C_{2}B_{2}\sim$矩形$ACC_{1}B_{1}$，…，按照此规律作下去，则边$AC_{2023}$的长为 ( )


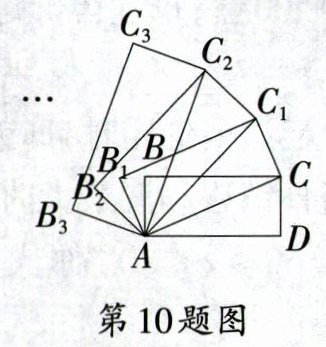
A. $\sqrt{5}\times(\frac{\sqrt{5}}{2})^{2023}$
B. $2\times(\frac{\sqrt{5}}{2})^{2022}$
C. $\sqrt{5}\times2^{2023}$
D. $2\times(\sqrt{5})^{2023}$

答案： A

11. 计算：$(\sqrt{2}+1)(\sqrt{2}-1)-\frac{\sqrt{6}}{\sqrt{3}}+2\sin45^{\circ}=$_______.

答案： 1

12. 如果关于x的一元二次方程$kx^{2}-\sqrt{3k + 1}x + 1 = 0$有两个不相等的实数根，那么k的取值范围是_______.

答案： $-\frac{1}{3}\leq k ＜ 1$且k ≠ 0

13. 如图,某古塔前有一棵高4 m的小树CD，发现水平地面上点E、树顶C和塔顶A恰好在一条直线上，测得BD = 57 m，D，E之间有一个花园距离无法测量；然后，在E处放置一平面镜，沿BE后退，退到G处恰好在平面镜中看到树顶C的像，EG = 2.4 m，测量者眼睛到地面的距离FG为1.6 m。已知$AB\perp BG$，$CD\perp BG$，$FG\perp BG$，点B，D，E，G在同一水平线上，则该古塔的高度AB为_______m.

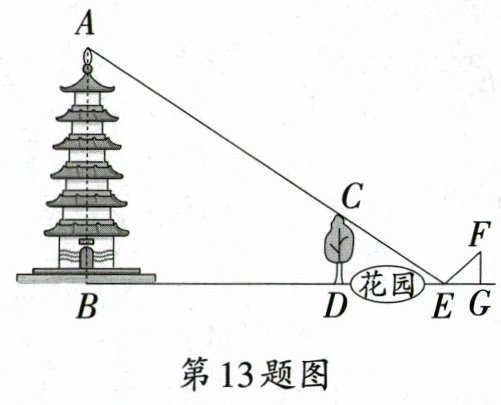
答案： 42

14. 如图,在菱形ABCD中，AC = 8，BD = 4，AC交BD于点O，E为OD的中点，连结CE并延长，交AD于点F，点G为CF的中点，连结OG，则OG = _______.

答案： $\frac{2\sqrt{5}}{3}$

15. 如图,在等腰直角三角形ABC中，$\angle BAC = 90^{\circ}$，AB = AC = 2，直角三角尺含45°角的顶点P在边BC上移动(点P不与B，C重合)，直角三角尺的一条直角边始终经过点A，斜边与边AC交于点Q。当△ABP为等腰三角形时，CQ的长为_______.

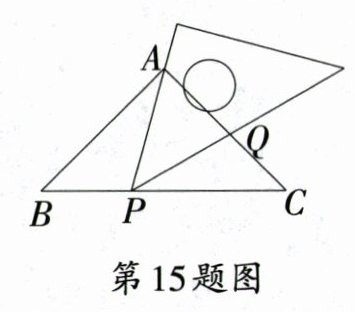
答案： 1或$2\sqrt{2}-2$