《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

1. 抛物线$y = x^{2}-2x + m$与$x$轴有两个交点，则$m$的取值范围为 ( )
A. $m ＞ 1$
B. $m = 1$
C. $m ＜ 1$
D. $m ＜ 4$

答案： C

2. 如图，以$(1,-4)$为顶点的二次函数$y = ax^{2}+bx + c$的图象与$x$轴负半轴交于点$A$，则一元二次方程$ax^{2}+bx + c = 0$的正数解的范围是 ( )
A. $2 ＜ x ＜ 3$ B. $3 ＜ x ＜ 4$ C. $4 ＜ x ＜ 5$ D. $5 ＜ x ＜ 6$
　

答案： C

3. 九下教材P34第15题改编 如图，小明在某次投篮中，球的运动路线是抛物线$y = -0.2x^{2}+3.5$的一部分. 若命中篮圈中心，则他与篮圈中心的水平距离$l$是 ( )


A. $3\ m$
B. $3.5\ m$
C. $4\ m$
D. $4.5\ m$

答案： C

4. 二次函数$y = x^{2}-8x + 15$的图象与$x$轴相交于$M$，$N$两点，点$P$在该函数的图象上运动，能使$\triangle PMN$的面积等于$\frac{1}{2}$的点$P$共有 ( )
A. $1$个
B. $2$个
C. $3$个
D. $4$个

答案： D

5. 〔绍兴市〕在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用$28\ m$长的篱笆围成一个矩形花园$ABCD$(篱笆只围$AB$，$BC$两边)，设$AB = m$. 若在$P$处有一棵树与墙$CD$，$AD$的距离分别是$15\ m$和$6\ m$，要将这棵树围在花园内(含边界，不考虑树的粗细)，则花园面积$S$的最大值为 ( )


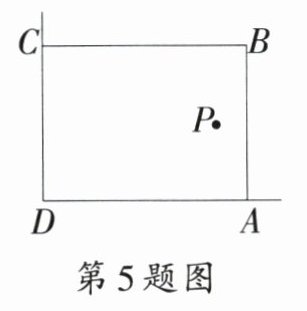
A. $193$
B. $194$
C. $195$
D. $196$

答案： C

6. 如图，抛物线$y = x^{2}-2x$与直线$y = 3$相交于点$A$，$B$，$P$是$x$轴上一点. 若$PA + PB$最小，则点$P$的坐标为 ( )


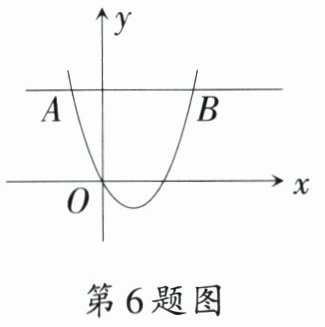
A. $(1,0)$
B. $(3,0)$
C. $(0,0)$
D. $(-1,0)$

答案：
A [解析]如图，作点B关于x轴的对称点B'，连结PA，PB，PB'，AB'，AB'与x轴交于点P'，则PB = PB'．
∵PA + PB = PA + PB'≥AB'，
∴当点P与点P'重合时，PA + PB取得最小值，为AB'的长．把y = 3代入y = x² - 2x，得x² - 2x = 3．解得x₁ = 3，x₂ = -1．
∴点A(-1，3)，B(3，3)．
∴点B'(3，-3)．设直线AB'的函数表达式为y = kx + b．把点A(-1，3)，B'(3，-3)代入，得$\begin{cases}-k + b = 3\\3k + b = -3\end{cases}$，解得$\begin{cases}k = -\frac{3}{2}\\b = \frac{3}{2}\end{cases}$．
∴y = -$\frac{3}{2}$x + $\frac{3}{2}$．在y = -$\frac{3}{2}$x + $\frac{3}{2}$中，当y = 0时，-$\frac{3}{2}$x + $\frac{3}{2}$ = 0．解得x = 1．
∴点P'(1，0)．
∴此时点P的坐标为(1，0)．故选A．

7. 〔朝霞原创〕如图所示，在平行四边形$ABCD$中，$AB = 3\ cm$，$BC = 6\ cm$，$\angle B = 60^{\circ}$，点$M$，$N$同时从点$B$出发，点$M$以$\sqrt{3}\ cm/s$的速度沿$B→A→D$运动，点$N$以$1\ cm/s$的速度沿$B→C$运动，当其中一点到达终点时，另一点也随之停止运动. 若$\triangle BMN$的面积为$y(cm^{2})$，运动时间为$x(s)$，则能够反映$y$与$x$之间函数关系的图象大致是 ( )

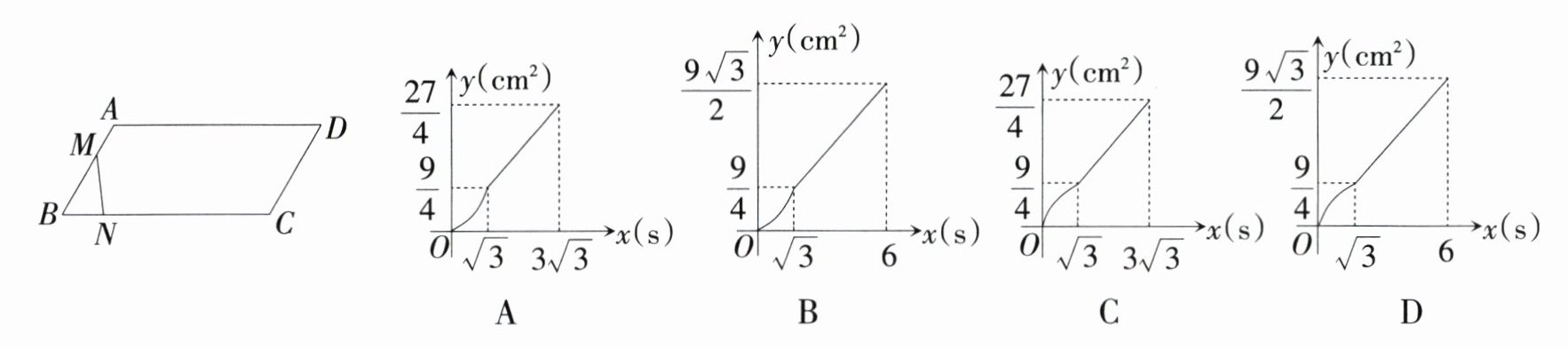
答案： A [解析]点M从点B运动到点A需要3÷$\sqrt{3}$ = $\sqrt{3}$(s)，从点A运动到点D需要6÷$\sqrt{3}$ = 2$\sqrt{3}$(s)，点N从点B运动到点C需要6÷1 = 6(s)．
∵$\sqrt{3}$ + 2$\sqrt{3}$ ＜ 6，
∴0≤x≤3$\sqrt{3}$．过点M作MG⊥BC于点G．
∵点M运动的路程为$\sqrt{3}$x cm，BN = x cm，
∴当0≤x≤$\sqrt{3}$时，MG = BM·sinB = $\sqrt{3}$x×$\frac{\sqrt{3}}{2}$ = $\frac{3}{2}$x．
∴y = $\frac{1}{2}$BN·MG = $\frac{1}{2}$x×$\frac{3}{2}$x = $\frac{3}{4}$x²．
∴此时y与x之间的函数图象为过原点，且开口向上的抛物线．当x = $\sqrt{3}$时，y = $\frac{3}{4}$×($\sqrt{3}$)² = $\frac{9}{4}$．当$\sqrt{3}$ ＜ x≤3$\sqrt{3}$时，过点A作AH⊥BC于点H．
∴AH = AB·sinB = 3×$\frac{\sqrt{3}}{2}$ = $\frac{3\sqrt{3}}{2}$．
∴y = $\frac{1}{2}$BN·AH = $\frac{1}{2}$x×$\frac{3\sqrt{3}}{2}$ = $\frac{3\sqrt{3}}{4}$x．此时y与x之间的函数图象为直线．当x = 3$\sqrt{3}$时，y = $\frac{3\sqrt{3}}{4}$×3$\sqrt{3}$ = $\frac{27}{4}$．综上所述，A选项符合题意．故选A．