2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (9分)如图,已知在$\triangle ABC$中,$\angle B = 45^{\circ}$,$CD$是$AB$边上的中线,$CD = 5$,$\sin\angle BCD=\frac{3}{5}$.
(1)求$BC$的长;
(2)求$\angle ACB$的正切值.

(1)求$BC$的长;
(2)求$\angle ACB$的正切值.

答案:
解:
(1)如图所示,过点D作DE⊥BC于点E.
∴∠BED = ∠CED = 90°.
∴∠B = ∠BDE = 45°.
∴BE = DE.
∵sin∠BCD = $\frac{DE}{CD}$ = $\frac{3}{5}$,CD = 5,
∴DE = BE = 3. 在Rt△CED中,由勾股定理,得CE = $\sqrt{CD² - DE²}$ = 4.
∴BC = BE + CE = 7.
(4分)

(2)如图所示,过点A作AF⊥BC于点F.
∴∠AFB = 90°.
∵∠BED = 90°,∠B = ∠B,
∴△BDE∽△BAF.
∵D为AB的中点,
∴$\frac{BD}{BA}$ = $\frac{DE}{AF}$ = $\frac{BE}{BF}$ = $\frac{1}{2}$.
∴AF = 2DE = 6,BF = 2BE = 6.
∴CF = BC - BF = 1.
∴在Rt△ACF中,tan∠ACB = $\frac{AF}{CF}$ = 6.
(9分)
解:
(1)如图所示,过点D作DE⊥BC于点E.
∴∠BED = ∠CED = 90°.
∴∠B = ∠BDE = 45°.
∴BE = DE.
∵sin∠BCD = $\frac{DE}{CD}$ = $\frac{3}{5}$,CD = 5,
∴DE = BE = 3. 在Rt△CED中,由勾股定理,得CE = $\sqrt{CD² - DE²}$ = 4.
∴BC = BE + CE = 7.
(4分)

(2)如图所示,过点A作AF⊥BC于点F.
∴∠AFB = 90°.
∵∠BED = 90°,∠B = ∠B,
∴△BDE∽△BAF.
∵D为AB的中点,
∴$\frac{BD}{BA}$ = $\frac{DE}{AF}$ = $\frac{BE}{BF}$ = $\frac{1}{2}$.
∴AF = 2DE = 6,BF = 2BE = 6.
∴CF = BC - BF = 1.
∴在Rt△ACF中,tan∠ACB = $\frac{AF}{CF}$ = 6.
(9分)
22. (10分)【综合与实践】小东在复习二次函数时,遇到这样一个问题:
如图1,一个横截面为抛物线形的公路隧道,其底部宽12 m,最大高度6 m.车辆双向通行,规定车辆必须在中心线两侧、距离道路边缘2 m的范围内行驶,并保持车辆顶部与隧道有不少于$\frac{1}{3}$ m的空隙.你能否根据这些要求,建立适当的平面直角坐标系,应用已有的函数知识,确定通过隧道车辆的高度限制?
如图2,小东以$O$点为原点,地面$OM$所在的直线为$x$轴建立平面直角坐标系,请你帮小东解决问题:
(1)求出这条抛物线的解析式,并注明自变量$x$的取值范围.
(2)求出通过隧道车辆的高度限制应为多少米?
(3)老师说:“隧道检修过程中,计划搭建一个由矩形$ABCD$的三条边$AD—DC—CB$组成的‘支撑架’,使$C$,$D$两点在抛物线上,$A$,$B$两点在地面$OM$上,如图3所示.”为了筹备材料,需求出这个“支撑架”三根木杆$AD$,$DC$,$CB$的长度之和的最大值是多少,请你帮忙计算一下.

如图1,一个横截面为抛物线形的公路隧道,其底部宽12 m,最大高度6 m.车辆双向通行,规定车辆必须在中心线两侧、距离道路边缘2 m的范围内行驶,并保持车辆顶部与隧道有不少于$\frac{1}{3}$ m的空隙.你能否根据这些要求,建立适当的平面直角坐标系,应用已有的函数知识,确定通过隧道车辆的高度限制?
如图2,小东以$O$点为原点,地面$OM$所在的直线为$x$轴建立平面直角坐标系,请你帮小东解决问题:
(1)求出这条抛物线的解析式,并注明自变量$x$的取值范围.
(2)求出通过隧道车辆的高度限制应为多少米?
(3)老师说:“隧道检修过程中,计划搭建一个由矩形$ABCD$的三条边$AD—DC—CB$组成的‘支撑架’,使$C$,$D$两点在抛物线上,$A$,$B$两点在地面$OM$上,如图3所示.”为了筹备材料,需求出这个“支撑架”三根木杆$AD$,$DC$,$CB$的长度之和的最大值是多少,请你帮忙计算一下.

答案:
解:
(1)
∵该公路隧道横截面为抛物线,其最大高度为6 m,底部宽度OM为12 m,
∴P(6,6).
设抛物线的解析式为y = a(x - 6)² + 6.
∵抛物线y = a(x - 6)² + 6经过点(0,0),
∴0 = a(0 - 6)² + 6.
解得a = -$\frac{1}{6}$.
∴抛物线的解析式为y = -$\frac{1}{6}$(x - 6)² + 6(0 ≤ x ≤ 12).
(3分)
(2)当x = 2时,y = -$\frac{1}{6}$(2 - 6)² + 6 = $\frac{10}{3}$.
∵$\frac{10}{3}$ - $\frac{1}{3}$ = 3(m),
∴通过隧道车辆的高度限制应为3 m.
(6分)
(3)设点A(m,0),则D$[m,-\frac{1}{6}(m - 6)² + 6]$,B(12 - m,0).
∴AD + DC + CB = 2AD + DC = 2×$[-\frac{1}{6}(m - 6)² + 6]$ + 12 - 2m = -$\frac{1}{3}m² + 2m + 12$ = -$\frac{1}{3}$(m - 3)² + 15.
(9分)
∵-$\frac{1}{3}$ < 0,
∴当m = 3时,AD + DC + CB有最大值,最大值是15.
∴这个“支撑架”三根木杆AD,DC,CB的长度之和的最大值是15 m.
(10分)
(1)
∵该公路隧道横截面为抛物线,其最大高度为6 m,底部宽度OM为12 m,
∴P(6,6).
设抛物线的解析式为y = a(x - 6)² + 6.
∵抛物线y = a(x - 6)² + 6经过点(0,0),
∴0 = a(0 - 6)² + 6.
解得a = -$\frac{1}{6}$.
∴抛物线的解析式为y = -$\frac{1}{6}$(x - 6)² + 6(0 ≤ x ≤ 12).
(3分)
(2)当x = 2时,y = -$\frac{1}{6}$(2 - 6)² + 6 = $\frac{10}{3}$.
∵$\frac{10}{3}$ - $\frac{1}{3}$ = 3(m),
∴通过隧道车辆的高度限制应为3 m.
(6分)
(3)设点A(m,0),则D$[m,-\frac{1}{6}(m - 6)² + 6]$,B(12 - m,0).
∴AD + DC + CB = 2AD + DC = 2×$[-\frac{1}{6}(m - 6)² + 6]$ + 12 - 2m = -$\frac{1}{3}m² + 2m + 12$ = -$\frac{1}{3}$(m - 3)² + 15.
(9分)
∵-$\frac{1}{3}$ < 0,
∴当m = 3时,AD + DC + CB有最大值,最大值是15.
∴这个“支撑架”三根木杆AD,DC,CB的长度之和的最大值是15 m.
(10分)
23. (10分)综合与探究
(1)【教材呈现】下面是华师版九上教材80页的一道习题,请完成证明.
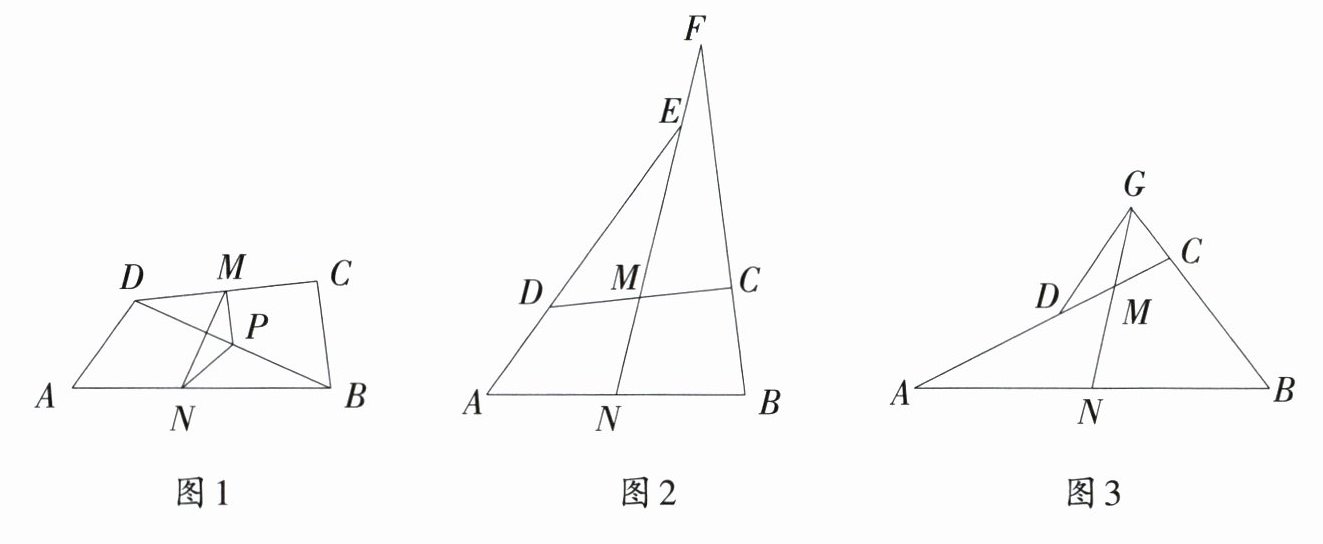
如图1,在四边形$ABCD$中,$AD = BC$,$P$是对角线$BD$的中点,$M$是$DC$的中点,$N$是$AB$的中点.
求证:$\angle PMN=\angle PNM$.
(2)【拓展延伸】
如图2,在四边形$ABCD$中,$AD = BC$,$M$是$DC$的中点,$N$是$AB$的中点,连结$NM$并延长分别与$AD$,$BC$的延长线交于点$E$,$F$.求证:$\angle AEN=\angle F$.
(3)【问题解决】
如图3,在$\triangle ABC$中,$AC\lt AB$,点$D$在$AC$上,$AD = BC$,$M$是$DC$的中点,$N$是$AB$的中点,连结$NM$并延长,与$BC$的延长线交于点$G$,连结$GD$.若$DC = 2$,当$\triangle CGD$是直角三角形时,直接写出$DG$的长.
(1)【教材呈现】下面是华师版九上教材80页的一道习题,请完成证明.
如图1,在四边形$ABCD$中,$AD = BC$,$P$是对角线$BD$的中点,$M$是$DC$的中点,$N$是$AB$的中点.
求证:$\angle PMN=\angle PNM$.
(2)【拓展延伸】
如图2,在四边形$ABCD$中,$AD = BC$,$M$是$DC$的中点,$N$是$AB$的中点,连结$NM$并延长分别与$AD$,$BC$的延长线交于点$E$,$F$.求证:$\angle AEN=\angle F$.
(3)【问题解决】
如图3,在$\triangle ABC$中,$AC\lt AB$,点$D$在$AC$上,$AD = BC$,$M$是$DC$的中点,$N$是$AB$的中点,连结$NM$并延长,与$BC$的延长线交于点$G$,连结$GD$.若$DC = 2$,当$\triangle CGD$是直角三角形时,直接写出$DG$的长.

答案:
解:
(1)证明:
∵P是对角线BD的中点,M是DC的中点,N是AB的中点,
∴PN = $\frac{1}{2}AD$,PM = $\frac{1}{2}BC$.
∵AD = BC,
∴PN = PM.
∴∠PMN = ∠PNM.
(3分)
(2)证明:如图①,连结BD,取BD的中点H,连结HM,HN.
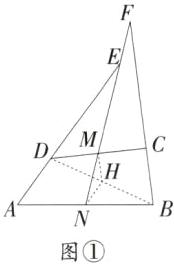
∵M是DC的中点,N是AB的中点,
∴HM//BC,HN//AD.
∴∠HMN = ∠F,∠AEN = ∠HNM.
由
(1)得∠HMN = ∠HNM.
∴∠AEN = ∠F.
(8分)
(3)当△CGD是直角三角形时,DG的长为$\sqrt{3}$或$\sqrt{5}$.
(10分)
【解析】如图②,连结BD,取BD的中点F,连结FM,FN.

由
(1)得∠FMN = ∠FNM.
同
(2)可知,FM//BG,FN//AM.
∴∠FMN = ∠CGM,∠FNM = ∠AMN.
∴∠CGM = ∠AMN.
∵∠AMN = ∠GMC,
∴∠CGM = ∠GMC.
∴CG = CM.
∵DC = 2,M是DC的中点,
∴DM = CM = $\frac{1}{2}CD$ = 1.
∴CG = CM = 1.
∵△CGD是直角三角形,
∴分两种情况:①当∠DGC = 90°时,
由勾股定理,得DG = $\sqrt{CD² - CG²}$ = $\sqrt{2² - 1²}$ = $\sqrt{3}$.
②当∠DCG = 90°时,
由勾股定理,得DG = $\sqrt{CD² + CG²}$ = $\sqrt{2² + 1²}$ = $\sqrt{5}$.
综上所述,当△CGD是直角三角形时,DG的长为$\sqrt{3}$或$\sqrt{5}$.
解:
(1)证明:
∵P是对角线BD的中点,M是DC的中点,N是AB的中点,
∴PN = $\frac{1}{2}AD$,PM = $\frac{1}{2}BC$.
∵AD = BC,
∴PN = PM.
∴∠PMN = ∠PNM.
(3分)
(2)证明:如图①,连结BD,取BD的中点H,连结HM,HN.

∵M是DC的中点,N是AB的中点,
∴HM//BC,HN//AD.
∴∠HMN = ∠F,∠AEN = ∠HNM.
由
(1)得∠HMN = ∠HNM.
∴∠AEN = ∠F.
(8分)
(3)当△CGD是直角三角形时,DG的长为$\sqrt{3}$或$\sqrt{5}$.
(10分)
【解析】如图②,连结BD,取BD的中点F,连结FM,FN.

由
(1)得∠FMN = ∠FNM.
同
(2)可知,FM//BG,FN//AM.
∴∠FMN = ∠CGM,∠FNM = ∠AMN.
∴∠CGM = ∠AMN.
∵∠AMN = ∠GMC,
∴∠CGM = ∠GMC.
∴CG = CM.
∵DC = 2,M是DC的中点,
∴DM = CM = $\frac{1}{2}CD$ = 1.
∴CG = CM = 1.
∵△CGD是直角三角形,
∴分两种情况:①当∠DGC = 90°时,
由勾股定理,得DG = $\sqrt{CD² - CG²}$ = $\sqrt{2² - 1²}$ = $\sqrt{3}$.
②当∠DCG = 90°时,
由勾股定理,得DG = $\sqrt{CD² + CG²}$ = $\sqrt{2² + 1²}$ = $\sqrt{5}$.
综上所述,当△CGD是直角三角形时,DG的长为$\sqrt{3}$或$\sqrt{5}$.
查看更多完整答案,请扫码查看


