2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
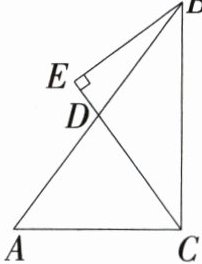
17. 如图,△ABC中,∠ACB = 90°,sinA = $\frac{4}{5}$,BC = 8,D是AB的中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
(1)求线段CD的长;
(2)求cos∠ABE的值.

答案:
解:
(1)$\because\angle ACB = 90^{\circ}$,$\therefore\sin A=\frac{BC}{AB}=\frac{4}{5}$.
$\because BC = 8$,$\therefore AB = 10$.
$\because D$是$AB$的中点,$\therefore CD=\frac{1}{2}AB = 5$.
(2)在$Rt\triangle ABC$中,$\because AB = 10$,$BC = 8$,
$\therefore AC=\sqrt{AB^{2}-BC^{2}} = 6$.
$\because D$是$AB$的中点,$\therefore BD = 5$,$S_{\triangle BDC}=S_{\triangle ADC}$.
$\therefore S_{\triangle BDC}=\frac{1}{2}S_{\triangle ABC}$,即$\frac{1}{2}CD\cdot BE=\frac{1}{2}\times\frac{1}{2}AC\cdot BC$.
$\therefore BE=\frac{24}{5}$.
在$Rt\triangle BDE$中,$\cos\angle ABE=\frac{BE}{BD}=\frac{\frac{24}{5}}{5}=\frac{24}{25}$.
(1)$\because\angle ACB = 90^{\circ}$,$\therefore\sin A=\frac{BC}{AB}=\frac{4}{5}$.
$\because BC = 8$,$\therefore AB = 10$.
$\because D$是$AB$的中点,$\therefore CD=\frac{1}{2}AB = 5$.
(2)在$Rt\triangle ABC$中,$\because AB = 10$,$BC = 8$,
$\therefore AC=\sqrt{AB^{2}-BC^{2}} = 6$.
$\because D$是$AB$的中点,$\therefore BD = 5$,$S_{\triangle BDC}=S_{\triangle ADC}$.
$\therefore S_{\triangle BDC}=\frac{1}{2}S_{\triangle ABC}$,即$\frac{1}{2}CD\cdot BE=\frac{1}{2}\times\frac{1}{2}AC\cdot BC$.
$\therefore BE=\frac{24}{5}$.
在$Rt\triangle BDE$中,$\cos\angle ABE=\frac{BE}{BD}=\frac{\frac{24}{5}}{5}=\frac{24}{25}$.
18. 日常生活情境 台灯 如图1,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB = 5 cm,连杆BC = CD = 20 cm,BC,CD与AB始终在同一平面内.
(1)如图2,转动连杆BC,CD,使∠BCD成平角,∠ABC = 143°,求连杆端点D离桌面l的高度DE;
(2)将图2中的连杆CD再绕点C逆时针旋转16°,如图3,此时连杆端点D离桌面l的高度减小了多少厘米?(结果保留到整数. 参考数据:sin37° ≈ 0.6,cos37° ≈ 0.8,tan37° ≈ 0.75.)

(1)如图2,转动连杆BC,CD,使∠BCD成平角,∠ABC = 143°,求连杆端点D离桌面l的高度DE;
(2)将图2中的连杆CD再绕点C逆时针旋转16°,如图3,此时连杆端点D离桌面l的高度减小了多少厘米?(结果保留到整数. 参考数据:sin37° ≈ 0.6,cos37° ≈ 0.8,tan37° ≈ 0.75.)

答案:
解:
(1)过点$B$作$BO\perp DE$于点$O$.
$\therefore\angle BOE=\angle BOD = 90^{\circ}$.
$\because DE\perp l$,$AB\perp l$,
$\therefore\angle OEA=\angle BAE = 90^{\circ}$,$EO// AB$.
$\therefore$四边形$ABOE$为矩形,$\angle D+\angle ABD = 180^{\circ}$.
$\therefore EO = AB = 5$.$\because\angle ABD = 143^{\circ}$,
$\therefore\angle D = 180^{\circ}-\angle ABD = 37^{\circ}$.
在$Rt\triangle BDO$中,$\angle BOD = 90^{\circ}$,$DB = CD + BC = 40$,
$\therefore DO = BD\cdot\cos D = 40\times\cos37^{\circ}\approx32$.
$\therefore DE = DO + EO = 37\text{ cm}$.
答:连杆端点$D$离桌面$l$的高度$DE$约为$37\text{ cm}$.
(2)如图,过点$D$作$DF\perp l$于点$F$,过点$C$作$CP\perp DF$于点$P$,过点$B$作$BG\perp DF$于点$G$,过点$C$作$CH\perp BG$于点$H$.
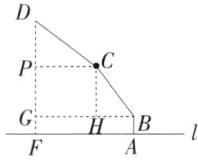
$\therefore$四边形$PCHG$和四边形$ABGF$是矩形.
$\therefore PG = CH$,$GF = AB$,$\angle PCH=\angle ABG = 90^{\circ}$.
$\therefore\angle CBH=\angle ABC-\angle ABG = 53^{\circ}$.
$\therefore\angle BCH = 90^{\circ}-\angle CBH = 37^{\circ}$.
$\because\angle BCD = 180^{\circ}-16^{\circ}=164^{\circ}$,
$\therefore\angle DCP=\angle BCD-\angle PCH-\angle BCH = 37^{\circ}$.
在$Rt\triangle CBH$中,$CH = BC\cdot\cos\angle BCH = 20\times\cos37^{\circ}\approx16$,
在$Rt\triangle DCP$中,$DP = CD\cdot\sin\angle DCP = 20\times\sin37^{\circ}\approx12$.
$\therefore DF = DP + PG + GF = DP + CH + AB = 12 + 16 + 5 = 33$.
$\therefore$下降高度为$37 - 33 = 4(\text{cm})$.
答:此时连杆端点$D$离桌面$l$的高度减小了$4\text{ cm}$.
解:
(1)过点$B$作$BO\perp DE$于点$O$.
$\therefore\angle BOE=\angle BOD = 90^{\circ}$.
$\because DE\perp l$,$AB\perp l$,
$\therefore\angle OEA=\angle BAE = 90^{\circ}$,$EO// AB$.
$\therefore$四边形$ABOE$为矩形,$\angle D+\angle ABD = 180^{\circ}$.
$\therefore EO = AB = 5$.$\because\angle ABD = 143^{\circ}$,
$\therefore\angle D = 180^{\circ}-\angle ABD = 37^{\circ}$.
在$Rt\triangle BDO$中,$\angle BOD = 90^{\circ}$,$DB = CD + BC = 40$,
$\therefore DO = BD\cdot\cos D = 40\times\cos37^{\circ}\approx32$.
$\therefore DE = DO + EO = 37\text{ cm}$.
答:连杆端点$D$离桌面$l$的高度$DE$约为$37\text{ cm}$.
(2)如图,过点$D$作$DF\perp l$于点$F$,过点$C$作$CP\perp DF$于点$P$,过点$B$作$BG\perp DF$于点$G$,过点$C$作$CH\perp BG$于点$H$.

$\therefore$四边形$PCHG$和四边形$ABGF$是矩形.
$\therefore PG = CH$,$GF = AB$,$\angle PCH=\angle ABG = 90^{\circ}$.
$\therefore\angle CBH=\angle ABC-\angle ABG = 53^{\circ}$.
$\therefore\angle BCH = 90^{\circ}-\angle CBH = 37^{\circ}$.
$\because\angle BCD = 180^{\circ}-16^{\circ}=164^{\circ}$,
$\therefore\angle DCP=\angle BCD-\angle PCH-\angle BCH = 37^{\circ}$.
在$Rt\triangle CBH$中,$CH = BC\cdot\cos\angle BCH = 20\times\cos37^{\circ}\approx16$,
在$Rt\triangle DCP$中,$DP = CD\cdot\sin\angle DCP = 20\times\sin37^{\circ}\approx12$.
$\therefore DF = DP + PG + GF = DP + CH + AB = 12 + 16 + 5 = 33$.
$\therefore$下降高度为$37 - 33 = 4(\text{cm})$.
答:此时连杆端点$D$离桌面$l$的高度减小了$4\text{ cm}$.
查看更多完整答案,请扫码查看


