《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

11. 写出一个一元二次方程，要求方程的一个根为0，另一个根为负数，满足条件的方程为____________.

答案： $x^2 + 2x = 0$（答案不唯一）

12.〔宜阳县〕若关于$x$的一元二次方程$x^{2}-6x - m = 0$有两个相等的实数根，则$m =$__________.

答案： -9

13. 设题新角度 过程性学习 解关于$x$的一元二次方程：$x^{2}=ax$. 下面是小聪的求解过程：
解：两边都减去$a^{2}$，得$x^{2}-a^{2}=ax - a^{2}$. ①
两边分别分解因式，得$(x + a)(x - a)=a(x - a)$. ②
两边都除以$x - a$，得$x + a = a$. ③
两边都减去$a$，得$x = 0$. ④
以上解题过程中，开始出现错误的那一步对应的序号是_________.

答案： ③

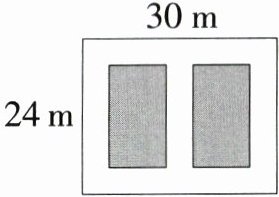
14.〔南阳市〕如图，某小区有一块长为30 m、宽为24 m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为$480m^{2}$，两块绿地之间及周边有宽度相等的人行通道，则人行通道的宽度为________m.

答案： 2

15.〔南通中考〕若$m,n$是一元二次方程$x^{2}+3x - 1 = 0$的两个实数根，则$\frac{m^{3}+m^{2}n}{3m - 1}$的值为________.

答案： 3 【一题多解】方法一：
∵$m$，$n$是一元二次方程$x^2 + 3x - 1 = 0$的两个实数根，
∴$m^2 + 3m - 1 = 0$，即$m^2 = -(3m - 1)$。解方程$x^2 + 3x - 1 = 0$，得$x_1 = \frac{-3 + \sqrt{13}}{2}$，$x_2 = \frac{-3 - \sqrt{13}}{2}$。
∴$m + n = -3$。
∴$\frac{m^3 + m^2n}{3m - 1} = \frac{m^2(m + n)}{3m - 1} = \frac{-(3m - 1)(m + n)}{3m - 1} = -(m + n) = 3$。
方法二：
∵$m$，$n$是一元二次方程$x^2 + 3x - 1 = 0$的两个实数根，
∴$m + n = -3$，$m^2 + 3m - 1 = 0$。
∴$3m - 1 = -m^2$。
∴$\frac{m^3 + m^2n}{3m - 1} = \frac{m^2(m + n)}{3m - 1} = \frac{-3m^2}{-m^2} = 3$。

16. 解方程：
(1)$2x^{2}-5x + 1 = 0$； (2)$3(x - 5)^{2}=4(5 - x)$.

答案： 解：
(1)$a = 2$，$b = -5$，$c = 1$。
$\Delta = b^2 - 4ac = (-5)^2 - 4\times2\times1 = 17$。
∴$x = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a} = \frac{5\pm\sqrt{17}}{2\times2} = \frac{5\pm\sqrt{17}}{4}$，
即$x_1 = \frac{5 + \sqrt{17}}{4}$，$x_2 = \frac{5 - \sqrt{17}}{4}$。
(2)移项，得$3(x - 5)^2 - 4(5 - x) = 0$。因式分解，得$(x - 5)(3x - 11) = 0$。于是得$x - 5 = 0$，或$3x - 11 = 0$，$x_1 = 5$，$x_2 = \frac{11}{3}$。

17. 已知一元二次方程$x^{2}-(2k + 1)x + k^{2}+k = 0$.
(1)求证：方程有两个不相等的实数根；
(2)若$\triangle ABC$的两边$AB,AC$的长是这个方程的两个实数根，第三边$BC$的长为5. 当$\triangle ABC$是等腰三角形时，求$k$的值.

答案： 解：
(1)证明：
∵$a = 1$，$b = -(2k + 1)$，$c = k^2 + k$，
∴$\Delta = [-(2k + 1)]^2 - 4(k^2 + k) = 1 ＞ 0$。
∴方程有两个不相等的实数根。
(2)根据题意，得$AB\neq AC$。
∵$\triangle ABC$为等腰三角形，
∴$AB$，$AC$中有一个值为5。
将$x = 5$代入原方程，得$25 - 5(2k + 1) + k^2 + k = 0$，
即$k^2 - 9k + 20 = 0$。
解得$k_1 = 4$，$k_2 = 5$。
当$k = 4$时，原方程为$x^2 - 9x + 20 = 0$。
解得$x_1 = 4$，$x_2 = 5$。符合题意。
当$k = 5$时，原方程为$x^2 - 11x + 30 = 0$。
解得$x_1 = 5$，$x_2 = 6$。符合题意。
综上所述，$k$的值为4或5。

18.〔鹤壁市〕(1)解答下列问题：①方程$x^{2}-x - 2 = 0$的解为______________；
②方程$x^{2}-2x - 3 = 0$的解为______________；
③方程$x^{2}-3x - 4 = 0$的解为______________.
(2)根据以上方程特征及其解的特征，请猜想：
①方程$x^{2}-9x - 10 = 0$的解为______________；
②关于$x$的方程______________的解为$x_{1}=-1,x_{2}=n + 1$.
(3)请用公式法解方程$x^{2}-9x - 10 = 0$，以验证猜想(2)中结论①的正确性.

答案： 解：
(1)①$x_1 = -1$，$x_2 = 2$ ②$x_1 = -1$，$x_2 = 3$ ③$x_1 = -1$，$x_2 = 4$
(2)①$x_1 = -1$，$x_2 = 10$ ②$x^2 - nx - (n + 1) = 0$
(3)$a = 1$，$b = -9$，$c = -10$。
∵$b^2 - 4ac = (-9)^2 - 4\times1\times(-10) = 121$，
∴$x = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a} = \frac{-(-9)\pm\sqrt{121}}{2\times1} = \frac{9\pm11}{2}$，即$x_1 = -1$，$x_2 = 10$。
∴猜想
(2)中结论①正确。