2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8.〔重庆市改编〕如图,四边形$ABCD$为平行四边形,$AF,BE$分别为$\angle DAB,\angle CBA$的平分线,且$AD = 2,AB = 3$,则$S_{\triangle EFG}:S_{\triangle ABF}=$( )
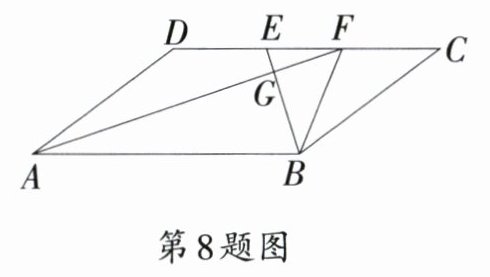
A. $2:3$
B. $1:9$
C. $1:12$
D. $4:9$

A. $2:3$
B. $1:9$
C. $1:12$
D. $4:9$
答案:
C [解析]
∵四边形ABCD是平行四边形,
∴AB//CD,AD = BC = 2,AB = CD = 3.
∴∠DFA = ∠FAB.
∵AF平分∠DAB,
∴∠DAF = ∠FAB.
∴∠DAF = ∠DFA.
∴DF = AD = 2.同理,可得CE = 2.
∴EF = DF + CE - CD = 1.
∵∠EGF = ∠AGB,
∴△EFG∽△BAG.
∴$\frac{EF}{AB}=\frac{FG}{AG}=\frac{1}{3}$.
∴$\frac{S_{\triangle EFG}}{S_{\triangle BAG}}=(\frac{1}{3})^2=\frac{1}{9}$,$\frac{S_{\triangle BAG}}{S_{\triangle BCF}}=\frac{AG}{FG}=3$.
∵$S_{\triangle ABF}=S_{\triangle BAG}+S_{\triangle BCF}$,
∴$S_{\triangle EFG}:S_{\triangle ABF}=1:12$.故选C.
∵四边形ABCD是平行四边形,
∴AB//CD,AD = BC = 2,AB = CD = 3.
∴∠DFA = ∠FAB.
∵AF平分∠DAB,
∴∠DAF = ∠FAB.
∴∠DAF = ∠DFA.
∴DF = AD = 2.同理,可得CE = 2.
∴EF = DF + CE - CD = 1.
∵∠EGF = ∠AGB,
∴△EFG∽△BAG.
∴$\frac{EF}{AB}=\frac{FG}{AG}=\frac{1}{3}$.
∴$\frac{S_{\triangle EFG}}{S_{\triangle BAG}}=(\frac{1}{3})^2=\frac{1}{9}$,$\frac{S_{\triangle BAG}}{S_{\triangle BCF}}=\frac{AG}{FG}=3$.
∵$S_{\triangle ABF}=S_{\triangle BAG}+S_{\triangle BCF}$,
∴$S_{\triangle EFG}:S_{\triangle ABF}=1:12$.故选C.
9.〔深圳市〕若$\frac{a}{b}=\frac{4}{3}$,则$\frac{a + 2b}{b}=$______。
答案:
$\frac{10}{3}$
10.〔南阳市〕如图,直线$AB// CD// EF$。若$AC = 4,CE = 3$,则$\frac{BD}{BF}$的值是______。


答案:
$\frac{4}{7}$
11.〔河南中考改编〕综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪$ABCD$为正方形,$AB = 30\mathrm{cm}$,顶点$A$处挂了一个铅锤$M$。如图是测量树高的示意图,测高仪上的点$D,A$与树顶$E$在一条直线上,铅垂线$AM$交$BC$于点$H$。经测量,点$A$距地面$1.8\mathrm{m}$,到树$EG$的距离$AF = 11\mathrm{m}$,$BH = 20\mathrm{cm}$。则树$EG$的高度为______$\mathrm{m}$。(结果精确到$0.1\mathrm{m}$)
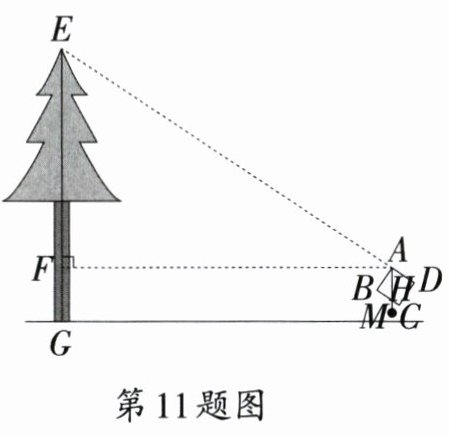

答案:
9.1 [解析]根据题意,得∠AFE = ∠ABH = 90°,∠BAE = ∠FAH = 90°.
∴∠EAF = 90° - ∠BAF = ∠HAB.
∴△AFE∽△ABH.
∴$\frac{EF}{BH}=\frac{AF}{AB}$.
∵AB = 30cm = 0.3m,BH = 20cm = 0.2m,AF = 11m,
∴$\frac{EF}{0.2}=\frac{11}{0.3}$.
∴$EF=\frac{22}{3}$m.
∴$EG = EF + 1.8=\frac{22}{3}+1.8\approx9.1$(m).
∴树EG的高度约为9.1m.
∴∠EAF = 90° - ∠BAF = ∠HAB.
∴△AFE∽△ABH.
∴$\frac{EF}{BH}=\frac{AF}{AB}$.
∵AB = 30cm = 0.3m,BH = 20cm = 0.2m,AF = 11m,
∴$\frac{EF}{0.2}=\frac{11}{0.3}$.
∴$EF=\frac{22}{3}$m.
∴$EG = EF + 1.8=\frac{22}{3}+1.8\approx9.1$(m).
∴树EG的高度约为9.1m.
12.〔濮阳市〕如图,在$\triangle ABC$中,$AB = 10\mathrm{cm},BC = 20\mathrm{cm}$,点$P$从点$A$开始沿$AB$边向点$B$以$1\mathrm{cm/s}$的速度移动,点$Q$从点$B$开始沿$BC$边向点$C$以$2\mathrm{cm/s}$的速度移动。如果点$P,Q$分别从点$A,B$同时出发,那么经过______$\mathrm{s}$时,以$B,P,Q$为顶点的三角形与$\triangle ABC$相似。
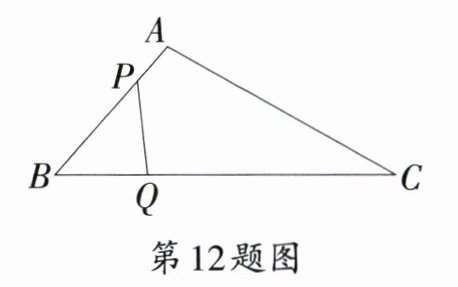

答案:
5或2 [解析]设经过t s时,以B,P,Q为顶点的三角形与△ABC相似.根据题意,得AP = t cm,BQ = 2t cm.
∵AB = 10 cm,
∴BP = (10 - t) cm.分两种情况:
①当△PBQ∽△ABC时,则$\frac{BP}{AB}=\frac{BQ}{BC}$,即$\frac{10 - t}{10}=\frac{2t}{20}$.解得t = 5.
②当△QBP∽△ABC时,则$\frac{BQ}{AB}=\frac{BP}{BC}$,即$\frac{2t}{10}=\frac{10 - t}{20}$.解得t = 2.
综上所述,经过5 s或2 s时,以B,P,Q为顶点的三角形与△ABC相似.
∵AB = 10 cm,
∴BP = (10 - t) cm.分两种情况:
①当△PBQ∽△ABC时,则$\frac{BP}{AB}=\frac{BQ}{BC}$,即$\frac{10 - t}{10}=\frac{2t}{20}$.解得t = 5.
②当△QBP∽△ABC时,则$\frac{BQ}{AB}=\frac{BP}{BC}$,即$\frac{2t}{10}=\frac{10 - t}{20}$.解得t = 2.
综上所述,经过5 s或2 s时,以B,P,Q为顶点的三角形与△ABC相似.
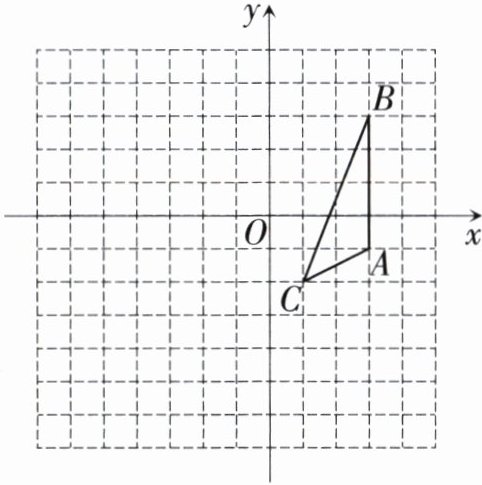
13. 如图,在平面直角坐标系中,$\triangle ABC$的三个顶点的坐标分别为$A(3,-1)$,$B(3,3)$,$C(1,-2)$。
(1)把$\triangle ABC$先向左平移$4$个单位长度,再向下平移$5$个单位长度,画出平移后的$\triangle A_{1}B_{1}C_{1}$;
(2)画出$\triangle ABC$关于$x$轴对称的$\triangle A_{2}B_{2}C_{2}$;
(3)画出$\triangle ABC$以点$O$为位似中心的位似图形$\triangle A_{3}B_{3}C_{3}$,使得$\triangle ABC$与$\triangle A_{3}B_{3}C_{3}$的位似比为$1:2$,并写出$\triangle A_{3}B_{3}C_{3}$各顶点的坐标。
(1)把$\triangle ABC$先向左平移$4$个单位长度,再向下平移$5$个单位长度,画出平移后的$\triangle A_{1}B_{1}C_{1}$;
(2)画出$\triangle ABC$关于$x$轴对称的$\triangle A_{2}B_{2}C_{2}$;
(3)画出$\triangle ABC$以点$O$为位似中心的位似图形$\triangle A_{3}B_{3}C_{3}$,使得$\triangle ABC$与$\triangle A_{3}B_{3}C_{3}$的位似比为$1:2$,并写出$\triangle A_{3}B_{3}C_{3}$各顶点的坐标。

答案:
解:
(1)△A₁B₁C₁如图所示.
(2)△A₂B₂C₂如图所示.
(3)△A₃B₃C₃如图所示.
点A₃(-6,2),点B₃(-6,-6),点C₃(-2,4).

解:
(1)△A₁B₁C₁如图所示.
(2)△A₂B₂C₂如图所示.
(3)△A₃B₃C₃如图所示.
点A₃(-6,2),点B₃(-6,-6),点C₃(-2,4).

查看更多完整答案,请扫码查看


