《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

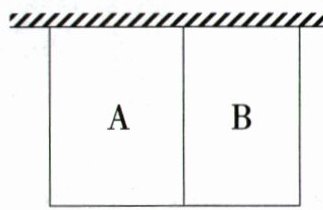
19. (9分)某学校为美化学校环境，打造绿色校园，决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园，用一道篱笆把花园分为A，B两块(如图所示)，花园里种满牡丹和芍药，学校已购买篱笆120 m. 如果花园的面积为1 200 m²，那么围成的花园与墙垂直的一边长为多少米？

答案： 解：设围成的花园与墙垂直的一边长为$x$m，则与墙平行的边的总长为$(120 - 3x)$m.
根据题意，得$x(120 - 3x)=1200$. (4分)
解得$x_{1}=x_{2}=20$.
答：围成的花园与墙垂直的一边长为20 m. (9分)

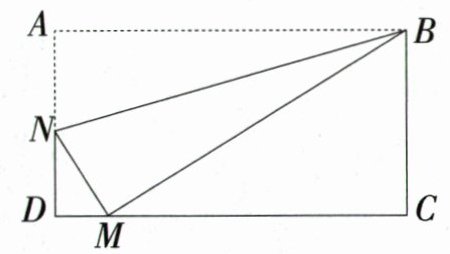
20. (9分)在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．有一张矩形纸片ABCD如图所示，点N在边AD上，现将矩形折叠，折痕为BN，点A对应的点为点M. 若点M恰好落在边DC上，则$\triangle MCB$与$\triangle NDM$是否相似？如果不相似，请说明理由；如果相似，请证明．

答案： 解：$\triangle MCB\sim\triangle NDM$. (1分)
证明：$\because$四边形$ABCD$是矩形，$\therefore\angle A=\angle D=\angle C = 90^{\circ}$. $\therefore\angle DNM+\angle DMN = 90^{\circ}$. (4分)
由折叠的性质可知，$\angle BMN=\angle A = 90^{\circ}$.
$\therefore\angle DMN+\angle CMB = 90^{\circ}$. $\therefore\angle CMB=\angle DNM$.
$\therefore\triangle MCB\sim\triangle NDM$. (9分)

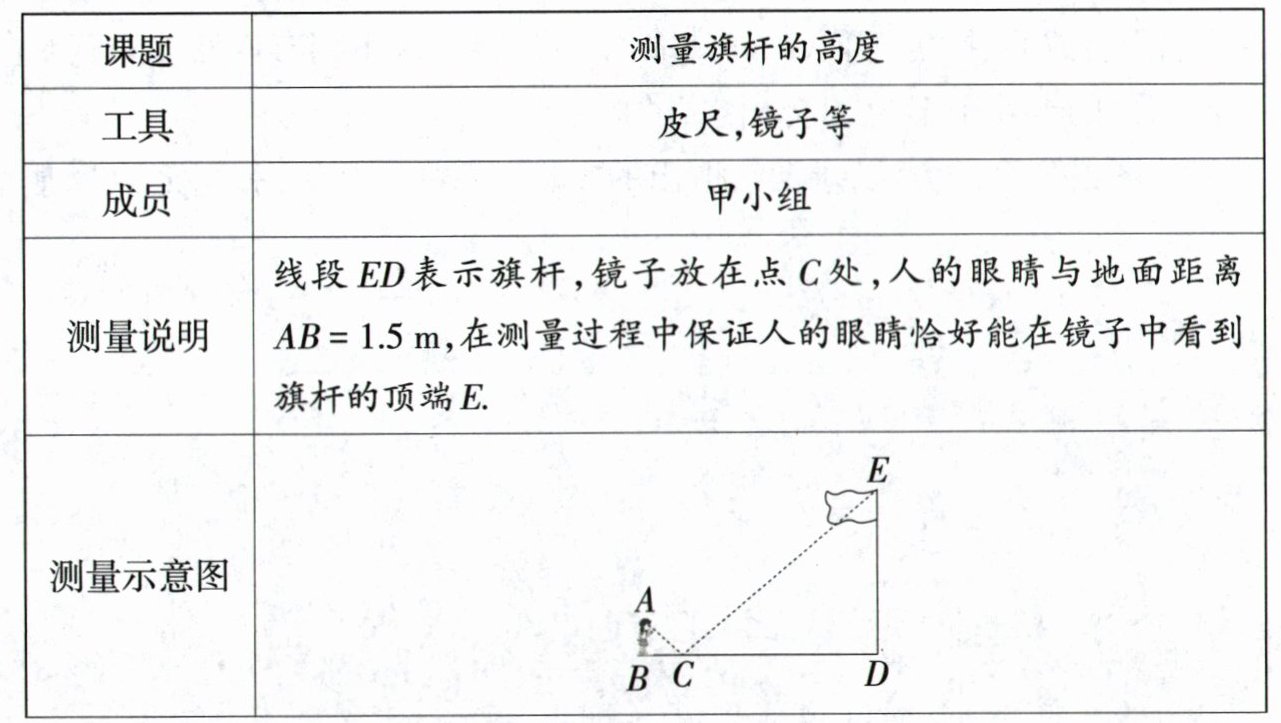
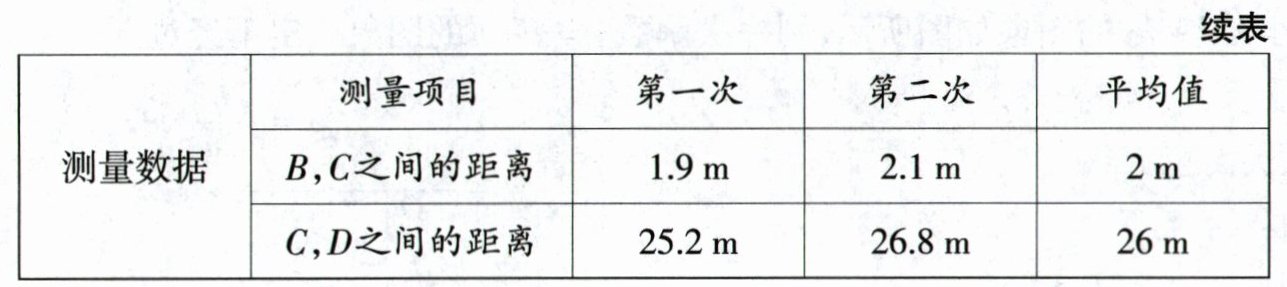
21. (9分)甲小组测量一旗杆的高度．为减小测量误差，在测量时，对每个数据都分别测量了两次并取它们的平均值作为测量结果，以下是他们测量报告的部分内容．


完成以下问题：
(1)甲小组这种测量方法的原理是我们所学的 ( )
A. 图形的平移 B. 图形的旋转 C. 图形的轴对称 D. 图形的相似
(2)根据以上测量结果，请求出旗杆的高度．(结果精确到1 m)

答案： 解：
(1)D (2分)
(2)由题意知，$\angle ACB=\angle DCE$，$BC = 2$m，$CD = 26$m，$AB = 1.5$m. (5分)
$\because\angle ABC=\angle EDC = 90^{\circ}$，$\therefore\triangle ACB\sim\triangle ECD$.
$\therefore\frac{AB}{DE}=\frac{BC}{CD}$，即$\frac{1.5}{DE}=\frac{2}{26}$.
$\therefore DE\approx20$m.
答：旗杆的高度约为20 m. (9分)