《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

19. （9分）【阅读理解】
爱思考的小明在解决问题：已知$a=\frac{1}{2+\sqrt{3}}$，求$2a^{2}-8a + 1$的值. 他是这样分析与解答的：
$\because a=\frac{1}{2+\sqrt{3}}=\frac{2 - \sqrt{3}}{(2+\sqrt{3})(2 - \sqrt{3})}=2 - \sqrt{3}$，$\therefore a - 2=-\sqrt{3}$.
$\therefore(a - 2)^{2}=3$，即$a^{2}-4a + 4 = 3$.
$\therefore a^{2}-4a=-1$.
$\therefore2a^{2}-8a + 1=2(a^{2}-4a)+1=2\times(-1)+1=-1$.
请你根据小明的分析过程，解决如下问题：
（1）计算：$\frac{1}{\sqrt{2}+1}$=_______；
（2）计算：$\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+\cdots+\frac{1}{\sqrt{100}+\sqrt{99}}$=_______；
（3）若$a=\frac{1}{\sqrt{5}-2}$，求$3a^{2}-12a - 1$的值.

答案： 解:
(1)$\sqrt{2}-1$　　　　　　　　　　(2分)
(2)9　　　　　　　　　　　　　　(5分)
[解析]原式 = $\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}+\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}+\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}+\cdots+\frac{\sqrt{100}-\sqrt{99}}{(\sqrt{100}+\sqrt{99})(\sqrt{100}-\sqrt{99})}$ = $\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+\cdots+\sqrt{100}-\sqrt{99}=\sqrt{100}-1 = 10 - 1 = 9$.
(3)
∵$a=\frac{1}{\sqrt{5}-2}=\frac{\sqrt{5}+2}{(\sqrt{5}-2)(\sqrt{5}+2)}=\sqrt{5}+2$，
∴$a - 2=\sqrt{5}$.
∴$(a - 2)^{2}=5$，即$a^{2}-4a + 4 = 5$.
∴$a^{2}-4a = 1$.　　　　　　　　　　　(7分)
　
∴$3a^{2}-12a - 1 = 3(a^{2}-4a)-1 = 3\times1 - 1 = 2$.　　　　　　　　　　　　　　(9分)

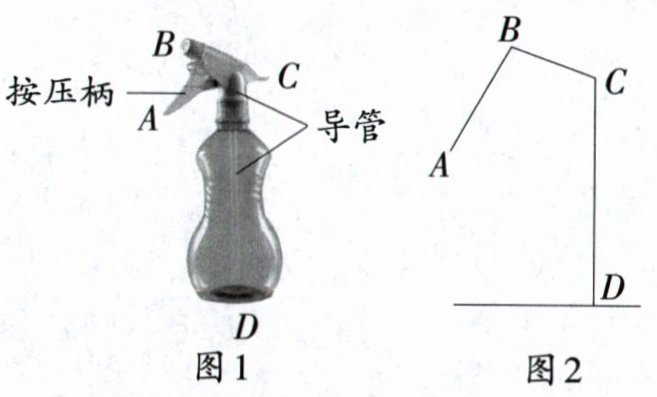
20. （9分）在学习过《解直角三角形》一章的知识后，九年级某班的同学们为了巩固学习成果，就地取材，利用所学的数学知识解决身边的问题. 如图1所示是教室内一只消毒用的酒精喷雾瓶的实物图，其示意图如图2所示，AB = 5 cm，BC = 4 cm，∠ABC = 100°，∠BCD = 110°. 求按压柄下端A到导管CD的距离.
（结果保留一位小数，参考数据：$\sin20^{\circ}\approx0.34$，$\cos20^{\circ}\approx0.94$，$\tan20^{\circ}\approx0.36$，$\sqrt{3}\approx1.73$.）

答案：
解:如图,过点A作AE⊥CD,垂足为E,过点B 作BF⊥DC,交DC的延长线于点F,过点A作AG⊥FB,交FB的延长线于点G.
　　　　　　　
　　由题意,得AE = FG,∠BFC = ∠AGB = 90°.
∵∠BCD是△BCF的一个外角，
　
∴∠FBC = ∠BCD - ∠BFC = 20°.
　在Rt△BCF中,BC = 4,
　
∴BF = BC·cos20°≈4×0.94 = 3.76.　(4分)
　
∵∠ABC = 100°,
　
∴∠ABG = 180° - ∠ABC - ∠FBC = 60°.
　
∵在Rt△ABG中,AB = 5,
　
∴BG = AB·cos60° = 5×$\frac{1}{2}$ = 2.5.
　
∴AE = FG = BG + BF = 2.5 + 3.76≈6.3(cm).答:按压柄下端A到导管CD的距离约为6.3cm.　　　　　　　　　　　　　(9分)