《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

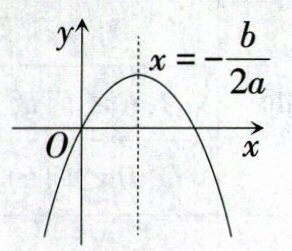
9. 二次函数$y = ax^{2}+bx$的图象如图所示，则一次函数$y = x + b$的图象一定不经过 ( )

A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： D 【解析】
∵二次函数的图象开口向下，$\therefore a＜0$.
∵对称轴$x = -\frac{b}{2a}＞0$，$\therefore b＞0$.
∴一次函数$y = x + b$的图象经过第一、二、三象限，不经过第四象限. 故选D.

10. 已知抛物线$y = x^{2}-2x - 1$，当$0\leqslant x\leqslant3$时，函数的最大值为 ( )
A. -2
B. -1
C. 0
D. 2

答案： D 【解析】$\because y = x^{2}-2x - 1=(x - 1)^{2}-2$，$\therefore$对称轴为直线$x = 1$. $\because1＞0$，$\therefore$抛物线的开口向上. $\because3 - 1＞1 - 0$，$\therefore$当$x = 3$时，$y$最大，此时$y = 9 - 6 - 1 = 2$. $\therefore$当$0\leqslant x\leqslant3$时，函数的最大值为2. 故选D.

11. 写出一个关于$x$的一元二次方程，使其一次项系数为-2，你写出的一元二次方程是____________________.

答案： $x^{2}-2x + 1 = 0$(答案不唯一)

12. 我国古代的“四书”是指《论语》《孟子》《大学》《中庸》，它们是儒家思想的核心著作，是我国传统文化的重要组成部分．如图，若从这四本著作中随机抽取两本(先随机抽取一本，不放回，再随机抽取另一本)，则抽取的两本恰好是《论语》和《大学》的概率是________.

答案： $\frac{1}{6}$

13. 若$\frac{a - b}{b}=\frac{2}{3}$，则$\frac{a}{b}=$________.

答案： $\frac{5}{3}$

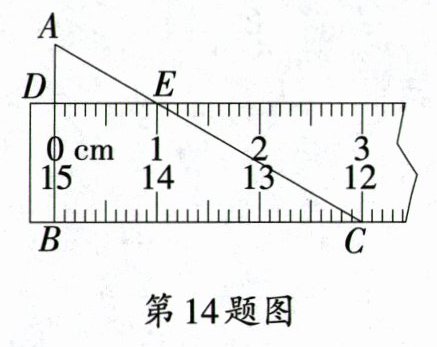
14. 如图，在$\triangle ABC$中，$\angle ABC = 90^{\circ}$，$\angle A = 60^{\circ}$，直尺的一边与$BC$重合，另一边分别交$AB$，$AC$于点$D$，$E$. 点$B$，$C$，$D$，$E$处的读数分别为15，12，0，1，则直尺宽$BD$的长为________.

答案： $\frac{2\sqrt{3}}{3}$cm 【解析】由题意得，$DE = 1$cm，$BC = 3$cm. $\because$在$Rt\triangle ABC$中，$\angle A = 60^{\circ}$，$\therefore AB=\frac{BC}{\tan60^{\circ}}=\frac{3}{\sqrt{3}}=\sqrt{3}$(cm). $\because DE// BC$，$\therefore\triangle ADE\sim\triangle ABC$. $\therefore\frac{DE}{BC}=\frac{AD}{AB}$，即$\frac{1}{3}=\frac{\sqrt{3}-BD}{\sqrt{3}}$. $\therefore BD=\frac{2\sqrt{3}}{3}$cm.

15. 在$\triangle ABC$中，$\angle B = 90^{\circ}$，$\angle A = 30^{\circ}$，$BC = 2$，$D$为$AB$的中点．若点$E$在边$AC$上，且$\frac{AD}{AB}=\frac{DE}{BC}$，则$AE$的长为________.

答案：
1或2 【解析】$\because$在$\triangle ABC$中，$\angle B = 90^{\circ}$，$\angle A = 30^{\circ}$，$BC = 2$，$\therefore AC = 2BC = 4$，$\angle C = 60^{\circ}$. $\therefore AB=\sqrt{AC^{2}-BC^{2}}=2\sqrt{3}$. $\because$点$D$为$AB$的中点，$\therefore AD=\frac{1}{2}AB=\sqrt{3}$. $\because\frac{AD}{AB}=\frac{DE}{BC}$，$\therefore DE=\frac{AD\cdot BC}{AB}=\frac{\sqrt{3}\times2}{2\sqrt{3}} = 1$.
分两种情况：①如图①，当$\angle ADE = 90^{\circ}$时，$\because\angle ADE=\angle ABC$，$\frac{AD}{AB}=\frac{DE}{BC}$，$\therefore\triangle ADE\sim\triangle ABC$. $\therefore\frac{AE}{AC}=\frac{AD}{AB}=\frac{1}{2}$. $\therefore AE=\frac{1}{2}AC = 2$.
　　　　　 　　
②如图②，当$\angle ADE\neq90^{\circ}$时，取$AC$的中点$H$，连结$DH$.
$\because D$是$AB$的中点，$H$是$AC$的中点，$\therefore DH// BC$，$DH=\frac{1}{2}BC = 1$. $\therefore\angle AHD=\angle C = 60^{\circ}$，$DH = DE = 1$. $\therefore\angle DEH = 60^{\circ}$. $\therefore\angle ADE=\angle DEH-\angle A = 30^{\circ}$. $\therefore\angle ADE=\angle A$. $\therefore AE = DE = 1$.
综上所述，$AE$的长为1或2.

16. (10分)计算：(1)$2^{-1}-\sqrt{\frac{1}{4}}+(2 - \sqrt{2})^{0}$； (2)$(\sqrt{12}+5\sqrt{8})\times\sqrt{3}$.

答案： 解：
(1)原式$=\frac{1}{2}-\frac{1}{2}+1$ (3分)
$= 1$. (5分)
(2)原式$=\sqrt{36}+5\sqrt{24}$ (3分)
$= 6 + 10\sqrt{6}$. (5分)