2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
16. (8分)解方程:
(1)$2x^{2}+x - 5 = 0$;
(2)$x(x + 8)=3(x + 8)$.
(1)$2x^{2}+x - 5 = 0$;
(2)$x(x + 8)=3(x + 8)$.
答案:
解:
(1)a = 2,b = 1,c = -5.
∴Δ = 1² - 4×2×(-5) = 41 > 0. (2分)
∴x = $\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}=\frac{-1\pm\sqrt{41}}{4}$,即x₁ = $\frac{-1 + \sqrt{41}}{4}$,x₂ = $\frac{-1 - \sqrt{41}}{4}$. (4分)
(2)移项,得x(x + 8) - 3(x + 8) = 0.
分解因式,得(x - 3)(x + 8) = 0. (2分)
∴x - 3 = 0,或x + 8 = 0,即x₁ = 3,x₂ = -8. (4分)
(1)a = 2,b = 1,c = -5.
∴Δ = 1² - 4×2×(-5) = 41 > 0. (2分)
∴x = $\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}=\frac{-1\pm\sqrt{41}}{4}$,即x₁ = $\frac{-1 + \sqrt{41}}{4}$,x₂ = $\frac{-1 - \sqrt{41}}{4}$. (4分)
(2)移项,得x(x + 8) - 3(x + 8) = 0.
分解因式,得(x - 3)(x + 8) = 0. (2分)
∴x - 3 = 0,或x + 8 = 0,即x₁ = 3,x₂ = -8. (4分)
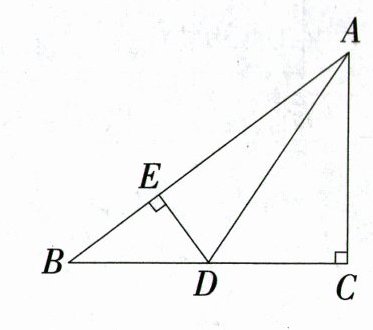
17. (9分)如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$D$是$BC$边上不同于$B,C$的一动点,过点$D$作$DE\perp AB$,垂足为点$E$,连结$AD$.
(1)求证:$\triangle DBE\sim\triangle ABC$;
(2)当$AC = 3$,$BC = 4$,$BD = 2$时,求$\triangle ADE$的面积.
(1)求证:$\triangle DBE\sim\triangle ABC$;
(2)当$AC = 3$,$BC = 4$,$BD = 2$时,求$\triangle ADE$的面积.

答案:
解:
(1)证明:
∵DE⊥AB,∠C = 90°,
∴∠BED = ∠C = 90°.
∵∠B = ∠B,
∴△DBE∽△ABC. (4分)
(2)在Rt△ABC中,∠C = 90°,AC = 3,BC = 4,
∴AB = $\sqrt{AC^{2}+BC^{2}} = 5$,S△ABC = $\frac{1}{2}$AC·BC = 6.
∵BD = 2,
∴S△ADB = $\frac{1}{2}$BD·AC = 3. (7分)
∵△DBE∽△ABC,
∴$\frac{S_{\triangle DBE}}{S_{\triangle ABC}} = (\frac{BD}{AB})^{2}=\frac{4}{25}$.
∴S△DBE = $\frac{4}{25}$S△ABC = $\frac{24}{25}$.
∴S△ADE = S△ADB - S△DBE = $\frac{51}{25}$. (9分)
(1)证明:
∵DE⊥AB,∠C = 90°,
∴∠BED = ∠C = 90°.
∵∠B = ∠B,
∴△DBE∽△ABC. (4分)
(2)在Rt△ABC中,∠C = 90°,AC = 3,BC = 4,
∴AB = $\sqrt{AC^{2}+BC^{2}} = 5$,S△ABC = $\frac{1}{2}$AC·BC = 6.
∵BD = 2,
∴S△ADB = $\frac{1}{2}$BD·AC = 3. (7分)
∵△DBE∽△ABC,
∴$\frac{S_{\triangle DBE}}{S_{\triangle ABC}} = (\frac{BD}{AB})^{2}=\frac{4}{25}$.
∴S△DBE = $\frac{4}{25}$S△ABC = $\frac{24}{25}$.
∴S△ADE = S△ADB - S△DBE = $\frac{51}{25}$. (9分)
18. (9分)某校数学活动小组要测量校园内一棵古树的高度,丹丹同学带领小组成员进行此项实践活动,记录如下:
填写人:丹丹 综合实践活动报告 时间:2023年12月15日
活动任务:测量古树高度
活动过程
[步骤一]设计测量方案:
小组成员讨论后,画出如图1的测量草图,确定需测的数据.
[步骤二]准备测量工具:
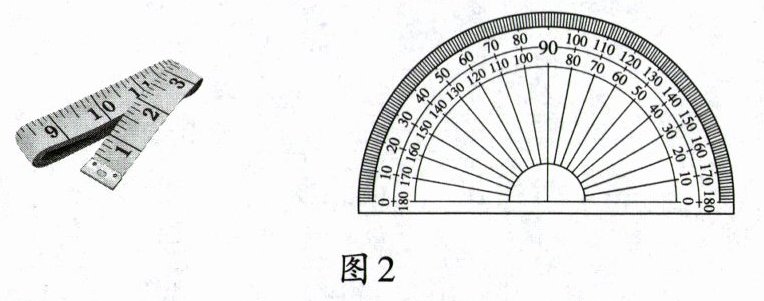
自制测角仪,把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角;准备皮尺,如图2所示.
[步骤三]实地测量并记录数据:
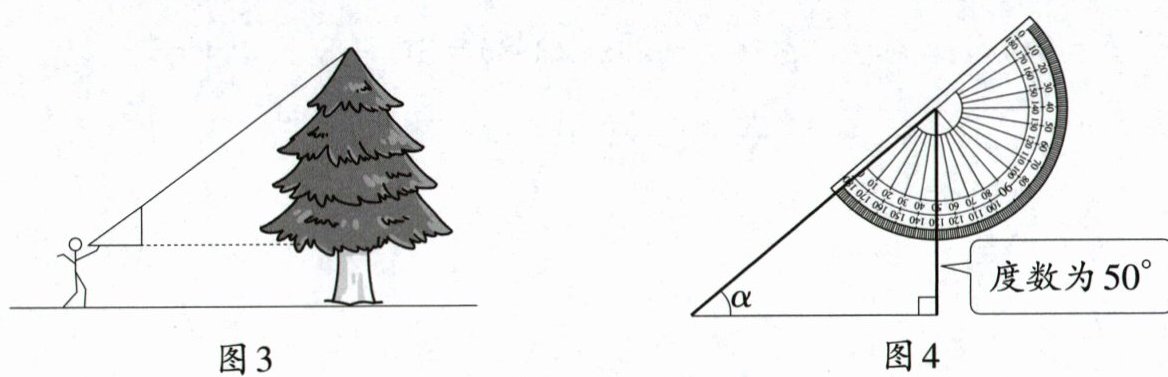
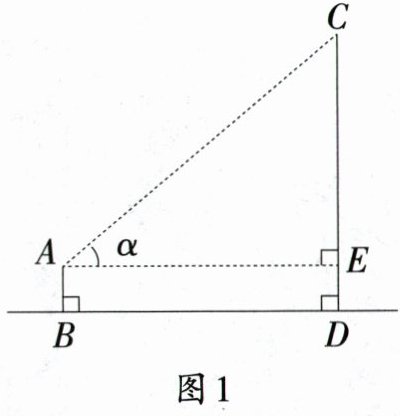
如图3,丹丹同学站在离古树一定距离的地方,将这个仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达古树的最高点.如图4,利用测角仪,测量后计算得出仰角$\alpha$,测出眼睛到地面的距离$AB$,测出所站地方到古树底部的距离$BD$.
$\alpha =$_______.经测量$AB = 1.54$m,$BD = 10$m.
[步骤四]计算古树高度$CD$.(结果精确到0.1 m.参考数据:$\sin40^{\circ}\approx0.643$,$\cos40^{\circ}\approx0.766$,$\tan40^{\circ}\approx0.839$.)
请结合图1、图4和相关数据写出$\alpha$的度数并完成[步骤四].
填写人:丹丹 综合实践活动报告 时间:2023年12月15日
活动任务:测量古树高度
活动过程
[步骤一]设计测量方案:
小组成员讨论后,画出如图1的测量草图,确定需测的数据.
[步骤二]准备测量工具:

自制测角仪,把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角;准备皮尺,如图2所示.
[步骤三]实地测量并记录数据:

如图3,丹丹同学站在离古树一定距离的地方,将这个仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达古树的最高点.如图4,利用测角仪,测量后计算得出仰角$\alpha$,测出眼睛到地面的距离$AB$,测出所站地方到古树底部的距离$BD$.
$\alpha =$_______.经测量$AB = 1.54$m,$BD = 10$m.
[步骤四]计算古树高度$CD$.(结果精确到0.1 m.参考数据:$\sin40^{\circ}\approx0.643$,$\cos40^{\circ}\approx0.766$,$\tan40^{\circ}\approx0.839$.)
请结合图1、图4和相关数据写出$\alpha$的度数并完成[步骤四].

答案:
解:
∵测角仪显示的度数为50°,
∴α = 90° - 50° = 40°. (3分)
∵AB⊥BD,ED⊥BD,CE⊥AE,
∴∠ABD = ∠EDB = ∠AED = 90°.
∴四边形ABDE是矩形. (5分)
∴AE = BD = 10 m,ED = AB = 1.54 m.
∴在Rt△CAE中,CE = AE·tanα = 8.39 m. (7分)
∴CD = CE + ED = 8.39 + 1.54 ≈ 9.9(m).
答:古树高度CD约为9.9 m. (9分)
∵测角仪显示的度数为50°,
∴α = 90° - 50° = 40°. (3分)
∵AB⊥BD,ED⊥BD,CE⊥AE,
∴∠ABD = ∠EDB = ∠AED = 90°.
∴四边形ABDE是矩形. (5分)
∴AE = BD = 10 m,ED = AB = 1.54 m.
∴在Rt△CAE中,CE = AE·tanα = 8.39 m. (7分)
∴CD = CE + ED = 8.39 + 1.54 ≈ 9.9(m).
答:古树高度CD约为9.9 m. (9分)
查看更多完整答案,请扫码查看


