《2025年王朝霞各地期末试卷精选九年级数学华师大版河南专版》

21. （10分）中秋节吃月饼是中国传统习俗. 在中秋节来临前，某超市购进一种品牌月饼，每盒进价是40元，并规定每盒售价不得少于50元，日销售量不低于350盒. 根据以往销售经验发现：当每盒售价定为50元时，日销售量为500盒；每盒售价每提高1元，日销售量减少10盒. 设每盒售价为x元，日销售量为p盒.
（1）当$x = 60$时，$p =$_______.
（2）当每盒售价定为多少元时，日销售利润W（元）最大？最大利润是多少元？
（3）小强说：“当日销售利润最大时，日销售额不是最大.”小红说：“当日销售利润不低于8000元时，每盒售价x的范围为$60\leq x\leq80$.”你认为他们的说法正确吗？若正确，请说明理由；若不正确，请求出正确的结论.

答案： 解:
(1)400
(2)根据题意，得p = 500 - 10(x - 50) = -10x + 1000.
∵日销售量不低于350盒，
-10x + 1000 ≥ 350. 解得x ≤ 65.
∵每盒售价不得少于50元，
∴x的取值范围为50 ≤ x ≤ 65.
根据题意，得W = (x - 40)(-10x + 1000) = -10x$^{2}+1400x - 40000=-10(x - 70)^{2}+9000$.
∵ -10 ＜ 0，
∴当50 ≤ x ≤ 65时，W随x增大而增大.
∴当x = 65时，W取得最大值，此时W = 8750.
答：当每盒售价定为65元时，日销售利润W最大，最大利润是8750元.
(3)小强正确，小红错误.
理由：设日销售额为y元.
根据题意，得y = x·p = x(-10x + 1000) = -10x$^{2}+1000x=-10(x - 50)^{2}+25000$.
∵ -10 ＜ 0，
∴当50 ≤ x ≤ 65时，y随x的增大而减小.
∴当x = 50时，y值最大，此时y = 25000.
当x = 65时，W值最大，此时W = 8750.
∴小强的说法正确.
令W = 8000，则-10(x - 70)$^{2}+9000 = 8000. 解得$x_{1}=60$，$x_{2}=80$.
结合函数图象可得当W≥8000时，60 ≤ x ≤ 80.
∵50 ≤ x ≤ 65，
∴当日销售利润不低于8000元时，60 ≤ x ≤ 65.
∴小红的说法错误，当日销售利润不低于8000元时，每盒售价x的范围为60 ≤ x ≤ 65.

22. （10分）揭示关系：如图1，在Rt△ABC中，$\angle C = 90^{\circ}$，$\angle A = 30^{\circ}$，BC = 1，AB = 2，$AC=\sqrt{3}$，即$BC:AC:AB = 1:\sqrt{3}:2$. 因此，对于含30°角的直角三角形的三边关系，可以作为问题解决的条件直接使用.
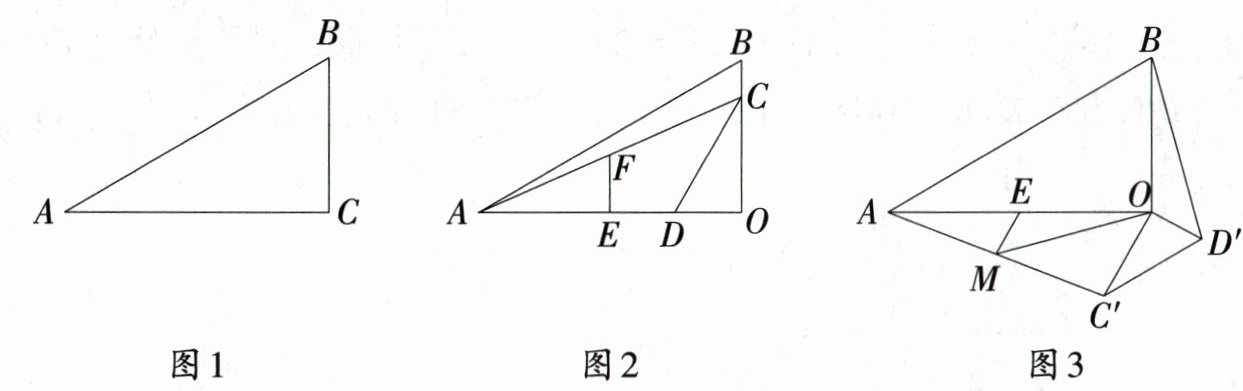
（1）问题解决：如图2，在Rt△AOB中，$\angle AOB = 90^{\circ}$，$\angle OAB = 30^{\circ}$，点C在边OB上，点D在边OA上，$\angle OCD = 30^{\circ}$，点E，F分别为OA，AC的中点. 则$\frac{EF}{OD}=$_______，$\frac{OE}{OB}=$_______.
（2）类比探究：将图2中△OCD绕点O逆时针旋转$\alpha(90^{\circ}＜\alpha＜180^{\circ})$后，得到△$OC'D'$，点C，D的对应点分别为点$C'$，$D'$，连结$AC'$，$BD'$，得到图3. 若点M是$AC'$的中点，连结OM.
①求证：△EOM∽△OBD'.
②线段OM和$BD'$之间存在怎样的数量关系和位置关系？写出你的结论，并进行证明.

答案： 解:
(1)$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$
(2)①证明:
∵点E，M分别是OA，$AC'$的中点，
∴EM是△$AOC'$的中位线.
∴EM//$OC'$，EM = $\frac{1}{2}OC'$.
∴∠OEM + ∠$AOC'=180^{\circ}$.
∵∠AOB = ∠$C'OD'=90^{\circ}$，
∴∠$BOD'+∠AOC'=180^{\circ}$.
∴∠OEM = ∠$BOD'$.
∵∠OAB = ∠$OC'D'=30^{\circ}$，
∴$\frac{EO}{EM}=\frac{\frac{1}{2}OA}{\frac{1}{2}OC'}=\frac{OA}{OC'}=\frac{\sqrt{3}OB}{\sqrt{3}OD'}=\frac{OB}{OD'}$.
∴$\frac{EO}{OB}=\frac{EM}{OD'}$.
∴△EOM∽△$OBD'$.
②结论：OM = $\frac{\sqrt{3}}{2}BD'$，OM⊥$BD'$.
证明：延长MO交$BD'$于点N.
由①可知，△EOM∽△$OBD'$.
∴∠EOM = ∠$OBD'$，$\frac{OM}{BD'}=\frac{EO}{OB}=\frac{\frac{1}{2}OA}{OB}=\frac{\frac{\sqrt{3}}{2}OB}{OB}=\frac{\sqrt{3}}{2}$.
∴OM = $\frac{\sqrt{3}}{2}BD'$.
∵∠AOB = $90^{\circ}$，
∴∠EOM + ∠BON = $180^{\circ}-∠AOB = 90^{\circ}$.
∴∠$OBD'+∠BON = 90^{\circ}$.
∴∠BNO = $90^{\circ}$.
∴OM⊥$BD'$.

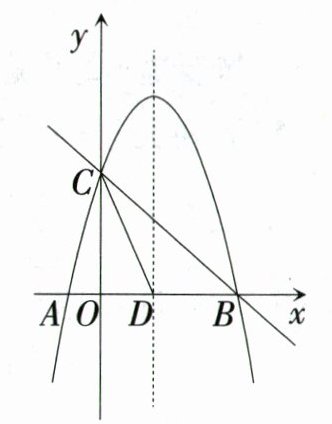
23. （10分）如图，抛物线$y = -x^{2}+bx + c$与x轴交于$A(-1,0)$，B两点，与y轴交于点$C(0,3)$，D是其对称轴与x轴的交点.
（1）求抛物线的表达式.
（2）在抛物线的对称轴上有一点M，使得$MA + MC$的值最小，求点M的坐标.
（3）在抛物线的对称轴上是否存在点P，使△PCD是等腰三角形？如果存在，请直接写出P点坐标；如果不存在，请说明理由.

答案： 解:
(1)将点C(0,3)，A(-1,0)代入y = $-x^{2}+bx + c$，得$\begin{cases}c = 3\\-1 - b + c = 0\end{cases}$，解得$\begin{cases}b = 2\\c = 3\end{cases}$.
∴抛物线的表达式为y = $-x^{2}+2x + 3$.
(2)连结MA，MB，BC.
∵y = $-x^{2}+2x + 3=-(x - 1)^{2}+4$，
∴抛物线的对称轴为直线x = 1.
∵点A，B关于直线x = 1对称，A(-1,0)，
∴点B的坐标为(3,0)，MA = MB.
∴MA + MC = MB + MC ≥ BC.
∴当B，C，M三点共线时，MA + MC取得最小值，最小值为BC的长.
设直线BC的表达式为y = kx + 3.
将(3,0)代入y = kx + 3，得3k + 3 = 0. 解得k = -1.
∴直线BC的表达式为y = -x + 3.令x = 1，则y = 2.
∴点M的坐标为(1,2).
(3)存在，点P的坐标为$(1,\frac{5}{3})$，(1,6)，(1,$\sqrt{10}$)或(1,-$\sqrt{10}$).
【解析】设点P的坐标为(1,t).
∵抛物线的对称轴为直线x = 1，
∴D(1,0).
∴OD = 1，$PD^{2}=t^{2}$.
∵C(0,3)，
∴OC = 3，$PC^{2}=1+(t - 3)^{2}$.
∵∠COD = $90^{\circ}$，
∴$CD^{2}=OC^{2}+OD^{2}=10$.
当△PCD是等腰三角形时，分三种情况：
①当PC = PD时，1 + (t - 3)$^{2}=t^{2}$. 解得t = $\frac{5}{3}$.
∴P$(1,\frac{5}{3})$.
②当PC = CD时，1 + (t - 3)$^{2}=10$. 解得$t_{1}=0$(舍去)，$t_{2}=6$.
∴P(1,6).
③当PD = CD时，$t^{2}=10$. 解得$t_{1}=\sqrt{10}$，$t_{2}=-\sqrt{10}$.
∴P(1,$\sqrt{10}$)或(1,-$\sqrt{10}$).
综上所述，点P的坐标为$(1,\frac{5}{3})$，(1,6)，(1,$\sqrt{10}$)或(1,-$\sqrt{10}$).