2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
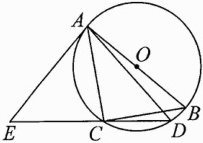
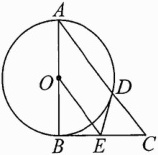
10.(2023乐山中考)如图,已知⊙O是Rt△ABC的外接圆,∠ACB = 90°,D是圆上一点,E是DC延长线上一点,连结AD、AE,且AD = AE,CA = CE.
(1)求证:直线AE是⊙O的切线;
(2)若sinE = $\frac{2}{3}$,⊙O的半径为3,求AD的长.
(1)求证:直线AE是⊙O的切线;
(2)若sinE = $\frac{2}{3}$,⊙O的半径为3,求AD的长.

答案:
(1)证明:
∵∠ACB = 90°,
∴AB是⊙O的直径,
∵AD = AE,
∴∠E = ∠D,
∵∠B = ∠D,
∴∠E = ∠B,
∵CA = CE,
∴∠E = ∠CAE,
∴∠CAE = ∠B,
∴∠OAE = ∠CAE + ∠CAB = ∠B + ∠CAB = 90°,
∴AE⊥AO,
∵OA是⊙O的半径,且AE⊥OA,
∴直线AE是⊙O的切线;
(2)解:作CF⊥AE于点F,则∠CFE = 90°,
∵∠E = ∠CAE = ∠B,
∴$\frac{CA}{AB}=\sin B=\sin E=\frac{CF}{CE}=\frac{2}{3}$,
∵OA = OB = 3,
∴AB = 6,
∴CE = CA = $\frac{2}{3}$AB = 4,
∴CF = $\frac{2}{3}$CE = $\frac{8}{3}$,
∴AF = EF = $\sqrt{CE^{2}-CF^{2}}=\frac{4\sqrt{5}}{3}$,
∴AD = AE = 2AF = $\frac{8\sqrt{5}}{3}$。
(1)证明:
∵∠ACB = 90°,
∴AB是⊙O的直径,
∵AD = AE,
∴∠E = ∠D,
∵∠B = ∠D,
∴∠E = ∠B,
∵CA = CE,
∴∠E = ∠CAE,
∴∠CAE = ∠B,
∴∠OAE = ∠CAE + ∠CAB = ∠B + ∠CAB = 90°,
∴AE⊥AO,
∵OA是⊙O的半径,且AE⊥OA,
∴直线AE是⊙O的切线;
(2)解:作CF⊥AE于点F,则∠CFE = 90°,
∵∠E = ∠CAE = ∠B,
∴$\frac{CA}{AB}=\sin B=\sin E=\frac{CF}{CE}=\frac{2}{3}$,
∵OA = OB = 3,
∴AB = 6,
∴CE = CA = $\frac{2}{3}$AB = 4,
∴CF = $\frac{2}{3}$CE = $\frac{8}{3}$,
∴AF = EF = $\sqrt{CE^{2}-CF^{2}}=\frac{4\sqrt{5}}{3}$,
∴AD = AE = 2AF = $\frac{8\sqrt{5}}{3}$。
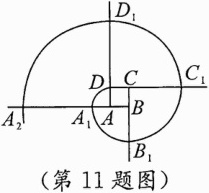
11.(2023达州中考)如图,四边形ABCD是边长为$\frac{1}{2}$的正方形,曲线DA₁B₁C₁D₁A₂…是由多段90°的圆心角所对的弧组成的,其中,$\overset{\frown}{DA_{1}}$的圆心为A,半径为AD;$\overset{\frown}{A_{1}B_{1}}$的圆心为B,半径为BA₁;$\overset{\frown}{B_{1}C_{1}}$的圆心为C,半径为CB₁;$\overset{\frown}{C_{1}D_{1}}$的圆心为D,半径为DC₁;…,$\overset{\frown}{DA_{1}}$、$\overset{\frown}{A_{1}B_{1}}$、$\overset{\frown}{B_{1}C_{1}}$、$\overset{\frown}{C_{1}D_{1}}$……的圆心依次为A、B、C、D循环,则$\overset{\frown}{A_{2023}B_{2023}}$的长是( )
A.$\frac{4045\pi}{2}$ B.2023π C.$\frac{2023\pi}{4}$ D.2022π
A.$\frac{4045\pi}{2}$ B.2023π C.$\frac{2023\pi}{4}$ D.2022π

答案:
A
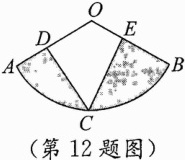
12.如图,半径为2的扇形ABO的圆心角为120°,点C是$\overset{\frown}{AB}$的中点,点D,E是半径OA,OB上的动点,且满足∠DCE = 60°,则图中阴影部分面积等于_________.

答案:
$\frac{4}{3}\pi-\sqrt{3}$
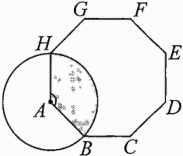
13.(2023菏泽中考)如图,正八边形ABCDEFGH的边长为4,以顶点A为圆心,AB的长为半径画圆,则阴影部分的面积为________(结果保留π).

答案:
6π
14.(2023广安中考)如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E是BC的中点,连结OE、DE.
(1)求证:DE是⊙O的切线;
(2)若sinC = $\frac{4}{5}$,DE = 5,求AD的长;
(3)求证:2DE² = CD·OE.
(1)求证:DE是⊙O的切线;
(2)若sinC = $\frac{4}{5}$,DE = 5,求AD的长;
(3)求证:2DE² = CD·OE.

答案:
(1)证明:连结OD,BD,在Rt△ABC中,∠ABC = 90°,
∵AB是⊙O的直径,
∴∠ADB = 90°,
∴∠BDC = 90°,
∵点E是BC的中点,
∴DE = BE = EC,
∵OB,OD是⊙O的半径,
∴OB = OD,又
∵OE = OE,
∴△ODE≌△OBE,
∴∠ODE = ∠OBE = 90°,
∵半径OD⊥DE,
∴DE是⊙O的切线;
(2)解:由
(1)知:DE = BE = EC,∠ADB = ∠BDC = ∠ABC = 90°,
∵DE = 5,
∴BC = 10,
∵$\sin C=\frac{4}{5}$,
∴$\frac{BD}{BC}=\frac{4}{5}$,
∴BD = 8,
∵∠C + ∠CBD = ∠ABD + ∠CBD = 90°,
∴∠ABD = ∠C,
∴$\sin\angle ABD=\sin C=\frac{4}{5}$,
∴$\frac{AD}{AB}=\frac{4}{5}$,设AD = 4x,AB = 5x,
∵AD² + BD² = AB²,
∴(4x)² + 8² = (5x)²,解得:x = $\frac{8}{3}$(负值舍去),
∴AD = 4x = 4×$\frac{8}{3}=\frac{32}{3}$;
(3)证明:由
(1)
(2)得:∠BDC = ∠OBE = 90°,BE = DE,
∵点O是AB的中点,点E是BC的中点,
∴OE//AC,BC = 2BE,
∴∠C = ∠OEB,
∴△BCD∽△OEB,
∴$\frac{CD}{BE}=\frac{BC}{OE}$,即$\frac{CD}{DE}=\frac{2DE}{OE}$,
∴2DE² = CD·OE。
(1)证明:连结OD,BD,在Rt△ABC中,∠ABC = 90°,
∵AB是⊙O的直径,
∴∠ADB = 90°,
∴∠BDC = 90°,
∵点E是BC的中点,
∴DE = BE = EC,
∵OB,OD是⊙O的半径,
∴OB = OD,又
∵OE = OE,
∴△ODE≌△OBE,
∴∠ODE = ∠OBE = 90°,
∵半径OD⊥DE,
∴DE是⊙O的切线;
(2)解:由
(1)知:DE = BE = EC,∠ADB = ∠BDC = ∠ABC = 90°,
∵DE = 5,
∴BC = 10,
∵$\sin C=\frac{4}{5}$,
∴$\frac{BD}{BC}=\frac{4}{5}$,
∴BD = 8,
∵∠C + ∠CBD = ∠ABD + ∠CBD = 90°,
∴∠ABD = ∠C,
∴$\sin\angle ABD=\sin C=\frac{4}{5}$,
∴$\frac{AD}{AB}=\frac{4}{5}$,设AD = 4x,AB = 5x,
∵AD² + BD² = AB²,
∴(4x)² + 8² = (5x)²,解得:x = $\frac{8}{3}$(负值舍去),
∴AD = 4x = 4×$\frac{8}{3}=\frac{32}{3}$;
(3)证明:由
(1)
(2)得:∠BDC = ∠OBE = 90°,BE = DE,
∵点O是AB的中点,点E是BC的中点,
∴OE//AC,BC = 2BE,
∴∠C = ∠OEB,
∴△BCD∽△OEB,
∴$\frac{CD}{BE}=\frac{BC}{OE}$,即$\frac{CD}{DE}=\frac{2DE}{OE}$,
∴2DE² = CD·OE。
查看更多完整答案,请扫码查看


