《2025年智慧学堂九年级数学下册华师大版》

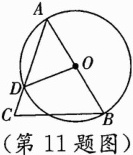
11.（泸州中考）如图，在△ABC中，AB为⊙O的直径，∠B = 60°，∠BOD = 100°，则∠C的度数为 （ ）

A. 50°
B. 60°
C. 70°
D. 80°

答案： C

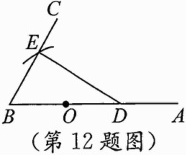
12.（贵阳中考）如图，已知∠ABC = 60°，点D为BA边上一点，BD = 10，点O为线段BD的中点，以点O为圆心，线段OB的长为半径作弧，交BC于点E，连结DE，则BE的长是 （ ）

A. 5
B. 5$\sqrt{2}$
C. 5$\sqrt{3}$
D. 5$\sqrt{5}$

答案： A

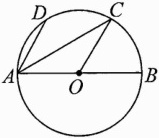
13. 如图，AB是⊙O的直径，点D，C在⊙O上，AD//OC，∠DAB = 70°，连结AC，则∠DAC等于________.

答案： 35°

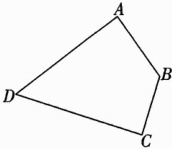
14. 如图，在四边形ABCD中，∠DAB = ∠DCB = 90°，试判断A、B、C、D四个点是否在同一个圆上，若在，说出圆心的位置，并画出这个圆.

答案： 解：A、B、C、D四个点在同一个圆上. 连结BD，取BD的中点O，连结OA、OC.
∵∠DAB=∠DCB=90°，
∴OA=OC=$\frac{1}{2}$BD，即OA=OB=OC=OD.
∴A、B、C、D四个点在以BD的中点O为圆心，BD长的一半为半径的圆上. 画圆略.

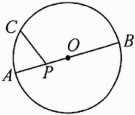
15. 如图，已知AB是⊙O的直径，P是OA上一点（不同于A，O），C是⊙O上的一点（不同于A，B），求证：PA＜PC＜PB.

答案： 证明：连结OC.
∵OA=OC，
∴PA=OA - OP=OC - OP＜PC，PB=OB + OP=OC + OP＞PC，
∴PA＜PC＜PB.

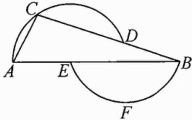
16. 如图，点D，E分别在△ABC的边BC，AB上，过A，C，D三点的圆的圆心为E，过B，F，E三点的圆的圆心为D，∠A = 63°，求∠B的度数.

答案： 解：连结EC，ED.
∵CE=AE，
∴∠ECA=∠A=63°，
∴∠AEC=180° - 63°×2 = 54°；
∵EC=ED，DE=DB，
∴∠ECD=∠EDC，∠DEB=∠B，设∠B=x°，则∠ECD=∠EDC=2x°，
∴x + 2x = 54，
∴x = 18，
∴∠B=18°.

17. 如图，已知正方形ABCD在半圆O内部，顶点A，B在圆上，C，D在直径上.
（1）求证：OD = OC.
（2）在正方形ABCD右侧再作一个小正方形ECGF，使点F在圆上，若正方形ABCD的边长为4，求正方形ECGF的边长.

答案：
(1)证明：连结OA，OB，
∵四边形ABCD是正方形，
∴∠ADO=∠BCO=90°，AD=BC. 又
∵OA=OB，
∴Rt△ADO≌Rt△BCO(HL)，
∴OD=OC.
(2)解：
∵BC=4，
∴OC=2，
∴OB=2$\sqrt{5}$，连结OF，设正方形ECGF的边长为x，则在Rt△OFG中FG²+OG²=OF²，即x²+(x + 2)²=(2$\sqrt{5}$)²，解得x₁=-4(舍去)，x₂=2，
∴正方形ECGF的边长为2.