2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11.在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O为圆心,OA长为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为 ( )
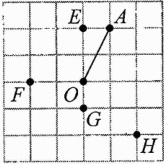
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F

A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
答案:
A
12.(2023广安中考)如图,△ABC内接于⊙O,圆的半径为7,∠BAC = 60°,则弦BC的长度为_________.
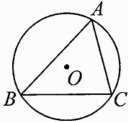

答案:
$7\sqrt{3}$
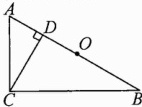
13.如图,在△ABC中,∠ACB = 90°,AB = 10,BC = 8,CD⊥AB于D,O为AB的中点.
(1)以C为圆心,6为半径作圆C,试判断A,D,B与⊙C的位置关系;
(2)⊙C的半径为多少时,点O在⊙C上?
(1)以C为圆心,6为半径作圆C,试判断A,D,B与⊙C的位置关系;
(2)⊙C的半径为多少时,点O在⊙C上?

答案:
解:$\because\angle ACB = 90^{\circ}$,$AB = 10$,$BC = 8$,$\therefore$易得$AC = 6$,$CD=\frac{24}{5}$.
(1)当以$6$为半径作$\odot C$时,$\because CA = 6$,$CD=\frac{24}{5}<6$,$CB = 8>6$,$\therefore$点$A$在$\odot C$上,点$D$在$\odot C$内,点$B$在$\odot C$外;
(2)$\because OC=\frac{1}{2}AB = 5$,$\therefore\odot C$的半径为$5$时,点$O$在$\odot C$上.
(1)当以$6$为半径作$\odot C$时,$\because CA = 6$,$CD=\frac{24}{5}<6$,$CB = 8>6$,$\therefore$点$A$在$\odot C$上,点$D$在$\odot C$内,点$B$在$\odot C$外;
(2)$\because OC=\frac{1}{2}AB = 5$,$\therefore\odot C$的半径为$5$时,点$O$在$\odot C$上.
14.(2023陕西中考)如图,△ABC内接于⊙O,∠BAC = 45°,过点B作BC的垂线,交⊙O于点D,并与CA的延长线交于点E,作BF⊥AC,垂足为M,交⊙O于点F.
(1)求证:BD = BC;
(2)若⊙O的半径r = 3,BE = 6,求线段BF的长.

(1)求证:BD = BC;
(2)若⊙O的半径r = 3,BE = 6,求线段BF的长.

答案:
(1)证明:连结$CD$,则$\angle BDC=\angle BAC = 45^{\circ}$,$\because BD\perp BC$,$\therefore\angle BCD = 90^{\circ}-\angle BDC = 45^{\circ}$,$\therefore\angle BCD=\angle BDC$,$\therefore BD = BC$;
(2)解:$\because\angle DBC = 90^{\circ}$,$\therefore CD$为$\odot O$的直径,$\therefore CD = 2r = 6$,$\therefore BC = CD\cdot\sin\angle BDC = 6\sin45^{\circ}=3\sqrt{2}$,$\therefore EC=\sqrt{BE^{2}+BC^{2}}=\sqrt{6^{2}+(3\sqrt{2})^{2}} = 3\sqrt{6}$.$\because\angle BMC=\angle EBC = 90^{\circ}$,$\angle BCM=\angle ECB$,$\therefore\triangle BCM\backsim\triangle ECB$,$\therefore\frac{EC}{EB}=\frac{BM}{CB}=\frac{CM}{EB}$,$\therefore BM=\frac{BC\cdot EB}{EC}=\frac{3\sqrt{2}\times6}{3\sqrt{6}} = 2\sqrt{3}$,$CM=\frac{BC^{2}}{EC}=\frac{(3\sqrt{2})^{2}}{3\sqrt{6}}=\sqrt{6}$,连结$CF$,则$\angle F=\angle BAC = 45^{\circ}$,$\therefore\angle MCF = 45^{\circ}$,$\therefore MF = MC=\sqrt{6}$,$\therefore BF = BM+MF = 2\sqrt{3}+\sqrt{6}$.
(1)证明:连结$CD$,则$\angle BDC=\angle BAC = 45^{\circ}$,$\because BD\perp BC$,$\therefore\angle BCD = 90^{\circ}-\angle BDC = 45^{\circ}$,$\therefore\angle BCD=\angle BDC$,$\therefore BD = BC$;
(2)解:$\because\angle DBC = 90^{\circ}$,$\therefore CD$为$\odot O$的直径,$\therefore CD = 2r = 6$,$\therefore BC = CD\cdot\sin\angle BDC = 6\sin45^{\circ}=3\sqrt{2}$,$\therefore EC=\sqrt{BE^{2}+BC^{2}}=\sqrt{6^{2}+(3\sqrt{2})^{2}} = 3\sqrt{6}$.$\because\angle BMC=\angle EBC = 90^{\circ}$,$\angle BCM=\angle ECB$,$\therefore\triangle BCM\backsim\triangle ECB$,$\therefore\frac{EC}{EB}=\frac{BM}{CB}=\frac{CM}{EB}$,$\therefore BM=\frac{BC\cdot EB}{EC}=\frac{3\sqrt{2}\times6}{3\sqrt{6}} = 2\sqrt{3}$,$CM=\frac{BC^{2}}{EC}=\frac{(3\sqrt{2})^{2}}{3\sqrt{6}}=\sqrt{6}$,连结$CF$,则$\angle F=\angle BAC = 45^{\circ}$,$\therefore\angle MCF = 45^{\circ}$,$\therefore MF = MC=\sqrt{6}$,$\therefore BF = BM+MF = 2\sqrt{3}+\sqrt{6}$.
15.(2023贵州中考)如图,已知⊙O是等边三角形ABC的外接圆,连结CO并延长交AB于点D,交⊙O于点E,连结EA,EB.
(1)写出图中一个度数为30°的角:_________,图中与△ACD全等的三角形是_________;
(2)求证:△AED∽△CEB;
(3)连结OA,OB,判断四边形OAEB的形状,并说明理由.
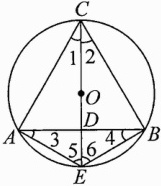
(1)写出图中一个度数为30°的角:_________,图中与△ACD全等的三角形是_________;
(2)求证:△AED∽△CEB;
(3)连结OA,OB,判断四边形OAEB的形状,并说明理由.

答案:
(1)$\angle 1$(或$\angle 2$,$\angle 3$,$\angle 4$);$\triangle BCD$;
(2)证明:$\because\triangle ABC$是等边三角形,$\therefore AC = BC$,$\therefore\overset{\frown}{AC}=\overset{\frown}{BC}$,$\therefore\angle 5=\angle 6$,$\because\angle 2=\angle 3$,$\therefore\triangle AED\backsim\triangle CEB$;
(3)解:四边形$OAEB$是菱形.理由:$\because\angle 5=\angle ABC = 60^{\circ}$,$OA = OE = OB$,$\therefore\triangle AOE$和$\triangle BOE$是边长相等的等边三角形,$\therefore OA = AE = BE = OB$,$\therefore$四边形$OAEB$是菱形.
(1)$\angle 1$(或$\angle 2$,$\angle 3$,$\angle 4$);$\triangle BCD$;
(2)证明:$\because\triangle ABC$是等边三角形,$\therefore AC = BC$,$\therefore\overset{\frown}{AC}=\overset{\frown}{BC}$,$\therefore\angle 5=\angle 6$,$\because\angle 2=\angle 3$,$\therefore\triangle AED\backsim\triangle CEB$;
(3)解:四边形$OAEB$是菱形.理由:$\because\angle 5=\angle ABC = 60^{\circ}$,$OA = OE = OB$,$\therefore\triangle AOE$和$\triangle BOE$是边长相等的等边三角形,$\therefore OA = AE = BE = OB$,$\therefore$四边形$OAEB$是菱形.
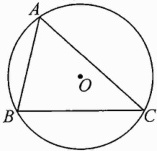
16.(凉山州中考)如图,⊙O的半径为R,其内接锐角三角形ABC中,∠A,∠B,∠C所对的边分别是a,b,c.
(1)求证:$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$;
(2)若∠A = 60°,∠C = 45°,BC = 4$\sqrt{3}$,利用(1)的结论求AB的长和sinB的值.
(1)求证:$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$;
(2)若∠A = 60°,∠C = 45°,BC = 4$\sqrt{3}$,利用(1)的结论求AB的长和sinB的值.

答案:
(1)证明:作直径$BE$,连结$CE$,则$\angle BCE = 90^{\circ}$,$\angle E=\angle A$,$\therefore\sin A=\sin E=\frac{BC}{BE}=\frac{a}{2R}$,$\therefore\frac{a}{\sin A}=2R$,同理:$\frac{b}{\sin B}=2R$,$\frac{c}{\sin C}=2R$,$\therefore\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$;
(2)解:由
(1)得:$\frac{AB}{\sin C}=\frac{BC}{\sin A}$,即$\frac{AB}{\sin45^{\circ}}=\frac{4\sqrt{3}}{\sin60^{\circ}} = 2R$,$\therefore AB=\frac{4\sqrt{3}\times\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}} = 4\sqrt{2}$,$2R=\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}} = 8$,过$B$作$BH\perp AC$于$H$,$\because\angle AHB=\angle BHC = 90^{\circ}$,$\therefore AH = AB\cdot\cos60^{\circ}=4\sqrt{2}\times\frac{1}{2}=2\sqrt{2}$,$CH=\frac{\sqrt{2}}{2}BC = 2\sqrt{6}$,$\therefore AC = AH+CH = 2(\sqrt{2}+\sqrt{6})$,$\therefore\sin B=\frac{AC}{2R}=\frac{2(\sqrt{2}+\sqrt{6})}{8}=\frac{\sqrt{2}+\sqrt{6}}{4}$.则$AB$的长为$4\sqrt{2}$,$\sin B$的值为$\frac{\sqrt{2}+\sqrt{6}}{4}$.
(1)证明:作直径$BE$,连结$CE$,则$\angle BCE = 90^{\circ}$,$\angle E=\angle A$,$\therefore\sin A=\sin E=\frac{BC}{BE}=\frac{a}{2R}$,$\therefore\frac{a}{\sin A}=2R$,同理:$\frac{b}{\sin B}=2R$,$\frac{c}{\sin C}=2R$,$\therefore\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$;
(2)解:由
(1)得:$\frac{AB}{\sin C}=\frac{BC}{\sin A}$,即$\frac{AB}{\sin45^{\circ}}=\frac{4\sqrt{3}}{\sin60^{\circ}} = 2R$,$\therefore AB=\frac{4\sqrt{3}\times\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}} = 4\sqrt{2}$,$2R=\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}} = 8$,过$B$作$BH\perp AC$于$H$,$\because\angle AHB=\angle BHC = 90^{\circ}$,$\therefore AH = AB\cdot\cos60^{\circ}=4\sqrt{2}\times\frac{1}{2}=2\sqrt{2}$,$CH=\frac{\sqrt{2}}{2}BC = 2\sqrt{6}$,$\therefore AC = AH+CH = 2(\sqrt{2}+\sqrt{6})$,$\therefore\sin B=\frac{AC}{2R}=\frac{2(\sqrt{2}+\sqrt{6})}{8}=\frac{\sqrt{2}+\sqrt{6}}{4}$.则$AB$的长为$4\sqrt{2}$,$\sin B$的值为$\frac{\sqrt{2}+\sqrt{6}}{4}$.
查看更多完整答案,请扫码查看


