《2025年智慧学堂九年级数学下册华师大版》

11. 四位同学在研究函数y=x²+bx+c(b，c是常数)时，甲发现当x=1时，函数有最小值；乙发现－1是方程x²+bx+c=0的一个根；丙发现函数的最小值为3；丁发现当x=2时，y=4. 已知这四位同学中只有一位发现的结论是错误的，则该同学是（ ）
A. 甲
B. 乙
C. 丙
D. 丁

答案： B

12. 设抛物线y=ax²+bx+c(a≠0)过A(0，2)，B(4，3)，C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为____________.

答案： $y = \frac{1}{8}x^2 - \frac{1}{4}x + 2$或$y = -\frac{1}{8}x^2+\frac{3}{4}x + 2$

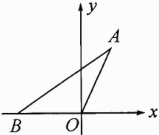
13. 如图，在平面直角坐标系xOy中，点A的坐标为(1，2)，△AOB的面积是2.
(1)求点B的坐标；
(2)求过点A，O，B的抛物线所对应的函数表达式.

答案： 解：
(1)点$B$的坐标为$(-2,0)$；
(2)$y = \frac{2}{3}x^2+\frac{4}{3}x$。

14. 已知抛物线y=ax²－2x+c的对称轴为直线x=－1，顶点为A，与y轴正半轴的交点为B，且△ABO的面积为1.
(1)求抛物线的表达式；
(2)若点P在x轴上，且PA=PB，求点P的坐标.

答案： 解：
(1)$\because$抛物线的对称轴为直线$x = - 1$，顶点为$A$，$\therefore -\frac{-2}{2a} = - 1$，$x_A = - 1$，$\therefore a = - 1$，$\because \triangle ABO$的面积为$1$，$\therefore \frac{1}{2}OB\cdot|x_A| = 1$，即$\frac{1}{2}c\times1 = 1$，$\therefore c = 2$，$\therefore$抛物线的表达式为$y = - x^2 - 2x + 2$；
(2)$\because y = - x^2 - 2x + 2 = -(x + 1)^2 + 3$，$\therefore A(-1,3)$，设点$P$的坐标为$(x,0)$，$\because PA = PB$，$B(0,2)$，$\therefore (x + 1)^2+3^2 = x^2 + 2^2$，解得$x = - 3$，$\therefore$点$P$的坐标为$(-3,0)$。

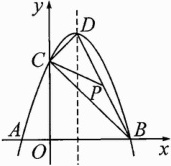
15. (牡丹江中考)已知抛物线y=－x²+bx+c与x轴交于A(－1，0)，B(3，0)两点，与y轴交于点C，顶点为D，如图.
(1)求抛物线的解析式；
(2)连结BC，CD，BD，P为BD的中点，连结CP，则线段CP的长是________.

答案： 解：
(1)$\because$抛物线$y = - x^2 + bx + c$与$x$轴交于$A(-1,0)$，$B(3,0)$两点，$\therefore$抛物线的解析式为$y = -(x + 1)(x - 3)$，即$y = - x^2 + 2x + 3$。
(2)$\sqrt{5}$

16. 已知抛物线y=ax²－2ax－3+2a²(a≠0).
(1)求这条抛物线的对称轴；
(2)若该抛物线的顶点在x轴上，求其解析式；
(3)设点P(m，y₁)，Q(3，y₂)在抛物线上，若y₁＜y₂，求m的取值范围.

答案： 解：
(1)$\because$抛物线$y = ax^2 - 2ax - 3 + 2a^2 = a(x - 1)^2 + 2a^2 - a - 3$，$\therefore$这条抛物线的对称轴为直线$x = 1$；
(2)$\because$抛物线的顶点在$x$轴上，$\therefore 2a^2 - a - 3 = 0$，解得$a=\frac{3}{2}$或$a = - 1$，$\therefore$抛物线的解析式为$y = \frac{3}{2}x^2 - 3x+\frac{3}{2}$或$y = - x^2 + 2x - 1$；
(3)$\because$抛物线的对称轴为直线$x = 1$，$\therefore Q(3,y_2)$关于直线$x = 1$的对称点的坐标为$(-1,y_2)$，$\therefore$当$a＞0$时，若$y_1＜y_2$，则$-1＜m＜3$；当$a＜0$，若$y_1＜y_2$，则$m＜-1$或$m＞3$。