《2025年智慧学堂九年级数学下册华师大版》

11. 如图，在同一平面直角坐标系中画出函数$y=\frac{1}{2}x^{2}$和函数$y = -\frac{1}{2}x^{2}$的图象，已知坐标原点$O$为正方形$ABCD$对角线的交点，且正方形的边分别与$x$轴、$y$轴平行，如果点$D$的坐标为$(2,2)$，那么阴影部分的面积为（ ）

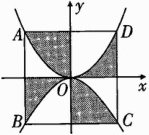
A. 4
B. 8
C. 12
D. 16

答案： B

12.（安徽六安月考）二次函数$y = ax^{2}$的图象如图所示，则不等式$ax＞a$的解集是（ ）

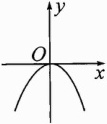
A. $x＞1$
B. $x＜1$
C. $x＞-1$
D. $x＜-1$

答案： B

13. 二次函数$y = ax^{2}$与一次函数$y = ax + a$在同一坐标系中的大致图象可能是（ ）

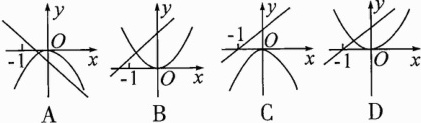
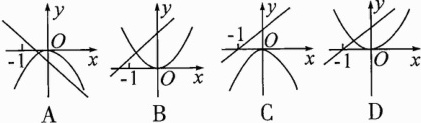
答案： D

14.（山东淄博高青一模）已知点$A(2,4)$，$B(0,1)$，点$M$在抛物线$y=\frac{1}{4}x^{2}$上运动，则$AM + BM$的最小值为_______.

答案： 5

15. 根据下列条件分别求$a$的取值范围：
(1)函数$y=(a - 2)x^{2}$，当$x＞0$时，$y$随$x$的增大而减小，当$x＜0$时，$y$随$x$的增大而增大；
(2)函数$y=(3a - 2)x^{2}$有最大值；
(3)抛物线$y=(a + 2)x^{2}$与$y = -\frac{1}{2}x^{2}$的形状相同；
(4)函数$y=(4a + 3)x^{2}$与$y = - 2x^{2}$的开口大小相同，但方向相反.

答案： 解：
(1)由题意得3a - 2 ＜ 0，解得a ＜ $\frac{2}{3}$；
(2)由题意得a - 2 ＜ 0，解得a ＜ 2；
(3)由题意得|a + 2| = | - $\frac{1}{2}$|，解得a = - $\frac{5}{2}$或a = - $\frac{3}{2}$；
(4)由题意得4a + 3 = 2，解得a = - $\frac{1}{4}$.

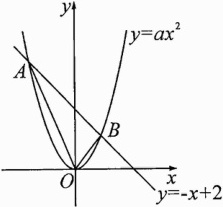
16. 如图，已知二次函数$y = ax^{2}$的图象与直线$y = - x + 2$交于点$A(-2,m)$，点$B$.
(1)求$m$，$a$的值；
(2)求点$B$的坐标；
(3)连结$OA$，$OB$，求$\triangle AOB$的面积.

答案： 解：
(1)将( - 2,m)代入y = - x + 2得m = 2 + 2 = 4，
∴点A的坐标为( - 2,4)，将( - 2,4)代入y = ax²得4 = 4a，解得a = 1；
(2)由
(1)知，二次函数的解析式为y = x²，令x² = - x + 2，解得x₁ = - 2，x₂ = 1，将x = 1代入y = x²得y = 1，
∴点B的坐标为(1,1)；
(3)设AB与y轴交于点E，将x = 0代入y = - x + 2得y = 2，
∴点E的坐标为(0,2)，
∴ OE = 2，
∴ S△AOB = $\frac{1}{2}$OE·|xA| + $\frac{1}{2}$OE·xB = $\frac{1}{2}$×2×2 + $\frac{1}{2}$×2×1 = 3.

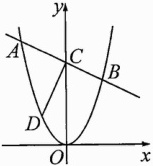
17. 如图，直线$y = -\frac{1}{2}x + b$与抛物线$y = ax^{2}$交于$A$，$B$两点，与$y$轴交于点$C$，其中点$A$的坐标为$(-4,8)$.
(1)求$a$，$b$的值；
(2)若$CD\perp AB$于点$C$，$CD = CA$. 试说明点$D$在抛物线上.

答案： 解：
(1)将( - 4,8)代入y = ax²得8 = 16a，解得a = $\frac{1}{2}$，把( - 4,8)代入y = - $\frac{1}{2}$x + b得8 = 2 + b，解得b = 6；
(2)过点A作AE⊥y轴于点E，DF⊥y轴于点F，
∵ CD⊥AB，
∴∠ACD = 90°，
∴∠ACE + ∠DCF = 90°，
∵∠ACE + ∠CAE = 90°，
∴∠DCF = ∠CAE，
∵ CD = CA，
∴△AEC≌△CFD，
∴ CE = DF，CF = AE = 4，将x = 0代入y = - $\frac{1}{2}$x + 6得y = 6，
∴点C的坐标为(0,6)，
∴ OC = 6，CE = DF = 8 - 6 = 2，
∵ OF = OC - CF = OC - AE = 6 - 4 = 2，
∴点D的坐标为( - 2,2)，把x = - 2代入y = $\frac{1}{2}$x²得y = 2，
∴点D在抛物线上.