《2025年智慧学堂九年级数学下册华师大版》

12. 如图，线段$AB$的长为2，点$C$为$AB$上一个动点，分别以$AC$，$BC$为斜边在$AB$的同侧作等腰直角三角形$ACD$和等腰直角三角形$BCE$，求$DE$长的最小值.

答案： 解：设$AC = x(0 ＜ x ＜ 2)$，则$BC = 2 - x$，$\because\triangle ACD$和$\triangle BCE$都是等腰直角三角形，$\therefore CD=\frac{\sqrt{2}}{2}x$，$CE=\frac{\sqrt{2}}{2}(2 - x)$，$\angle DCA=\angle ECB = 45^{\circ}$，$\therefore\angle DCE = 180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$，在$Rt\triangle DCE$中，由勾股定理，得$DE^{2}=DC^{2}+CE^{2}=(\frac{\sqrt{2}}{2}x)^{2}+[\frac{\sqrt{2}}{2}(2 - x)]^{2}=x^{2}-2x + 2=(x - 1)^{2}+1$，$\therefore$当$x = 1$时，$DE^{2}$有最小值1，此时$DE = 1$，故$DE$长的最小值为1.

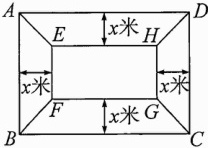
13. 有一块矩形地块$ABCD$，$AB = 20$米，$BC = 30$米. 为了美观，拟种植不同的花卉，如图所示，将矩形$ABCD$分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为$x$米. 现决定在等腰梯形$AEHD$和$BCGF$中种植甲种花卉；在等腰梯形$ABFE$和$CDHG$中种植乙种花卉；在矩形$EFGH$中种植丙种花卉. 甲、乙、丙三种花卉的种植成本分别为20元/平方米、60元/平方米、40元/平方米，设三种花卉的种植总成本为$y$元.
(1)当$x = 5$时，求种植总成本；
(2)求$y$与$x$的函数解析式，并写出自变量$x$的取值范围；
(3)若甲、乙两种花卉的种植面积之差不超过120平方米，求三种花卉的最低种植总成本.

答案：
解：
(1)当$x = 5$时，$EF = 20 - 2\times5 = 10$(米)，$EH = 30 - 2\times5 = 20$(米)，$\therefore y = 2\times\frac{1}{2}(EH + AD)\times x\times20 + 2\times\frac{1}{2}(EF + AB)\times x\times60+EF\cdot EH\times40=(20 + 30)\times5\times20+(10 + 20)\times5\times60+10\times20\times40 = 22000$，$\therefore$当$x = 5$时，种植总成本为22000元；
(2)由题易知$EF=(20 - 2x)$米，$EH=(30 - 2x)$米，则$y = 2\times\frac{1}{2}\times(30 + 30 - 2x)\times x\times20+2\times\frac{1}{2}\times(20 + 20 - 2x)\times x\times60+(30 - 2x)(20 - 2x)\times40=-400x + 24000(0 ＜ x ＜ 10)$；
(3)$S_{甲}=2\times\frac{1}{2}(EH + AD)\times x=(30 - 2x + 30)x=-2x^{2}+60x$. 同理，$S_{乙}=-2x^{2}+40x$.$\because$甲、乙两种花卉的种植面积之差不超过120平方米，$\therefore - 2x^{2}+60x-(-2x^{2}+40x)\leq120$，解得$x\leq6$，故$0 ＜ x\leq6$.$\because y=-400x + 24000$，$\therefore y$随$x$的增大而减小，$\therefore$当$x = 6$时，$y$有最小值为21600，即三种花卉的最低种植总成本为21600元.

14. (绍兴中考)已知函数$y = -x^{2}+bx + c(b,c$为常数)的图象经过点$(0,-3)$，$(-6,-3)$.
(1)求$b$，$c$的值；
(2)当$-4\leqslant x\leqslant0$时，求$y$的最大值；
(3)当$m\leqslant x\leqslant0$时，若$y$的最大值与最小值之和为2，求$m$的值.

答案： 解：
(1)把点$(0,-3)$，$(-6,-3)$的坐标分别代入$y=-x^{2}+bx + c$，解得$b=-6$，$c=-3$；
(2)$y=-x^{2}-6x - 3=-(x + 3)^{2}+6$，$\because - 4\leq x\leq m$，当$x = - 3$时，$y$取得最大值，最大值为6；
(3)①若$-3 ＜ m\leq0$，当$x = 0$时，$y$取得最小值，最小值为$-3$；当$x = m$时，$y$取得最大值，最大值为$-m^{2}-6m - 3$，$\therefore - m^{2}-6m - 3+(-3)=2$，解得$m=-2$或$m=-4$(舍去). ②若$m\leq - 3$，当$x=-3$时，$y$取得最大值，最大值为6，$\because y$的最大值与最小值之和为2，$\therefore y$的最小值为$-4$，$\therefore-(m + 3)^{2}+6=-4$，解得$m=-3-\sqrt{10}$或$m=-3+\sqrt{10}$(舍去)，综上所述，$m=-2$或$m=-3-\sqrt{10}$.