《2025年智慧学堂九年级数学下册华师大版》

1. 下列说法中，不正确的是 （ ）
A. 正多边形一定有一个外接圆和一个内切圆
B. 各边相等且各角相等的多边形是正多边形
C. 正多边形的内切圆和外接圆是同心圆
D. 既是轴对称图形又是中心对称图形的多边形是正多边形

答案： D

2. 已知圆内接正三角形的面积为3$\sqrt{3}$，则边心距是 （ ）
A. 2
B. 1
C. $\sqrt{3}$
D. $\frac{\sqrt{3}}{2}$

答案： B

3.（成都中考）如图，正六边形ABCDEF内接于⊙O. 若⊙O的周长等于6π，则正六边形的边长为 （ ）

A. $\sqrt{3}$
B. $\sqrt{6}$
C. 3
D. 2$\sqrt{3}$

答案： C

4.（2023德阳中考）已知一个正多边形的边心距与边长之比为$\frac{\sqrt{3}}{2}$，则这个正多边形的边数是 （ ）
A. 4
B. 6
C. 7
D. 8

答案： B

5.（2023内江中考）如图，正六边形ABCDEF内接于⊙O，点P在⌢AB上，点Q是⌢DE的中点，则∠CPQ的度数为 （ ）

A. 30°
B. 45°
C. 36°
D. 60°

答案： B

6. 如图所示，AB，CD是⊙O中互相垂直的两条直径，以A为圆心，AO为半径画弧，与⊙O交于E，F两点.
（1）求证：AE是⊙O的内接正六边形的一边；
（2）请在图上继续画出这个正六边形.

答案：
(1)证明:连结 OE，
∵AE = OA = OE，
∴△AOE 是等边三角形，
∴∠AOE = 60°，
∴AE 是⊙O 的内接正六边形的一边；
(2)画图略.

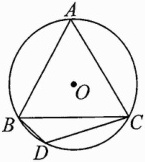
7. 如图，已知等边△ABC内接于⊙O，BD为内接正十二边形的一边，CD = 5$\sqrt{2}$ cm，求⊙O的半径R.

答案： 解:连结 OB，OC，OD，
∵等边△ABC 内接于⊙O，BD 为内接正十二边形的一边，
∴∠BOC = $\frac{1}{3}\times360^{\circ}=120^{\circ}$，∠BOD = $\frac{1}{12}\times360^{\circ}=30^{\circ}$，
∴∠COD = ∠BOC - ∠BOD = 90°，
∵OC = OD，
∴∠OCD = 45°，
∴OC = CD·cos45° = $5\sqrt{2}\times\frac{\sqrt{2}}{2}=5$(cm)，即⊙O 的半径 R 为 5 cm.

8. 请阅读下列材料，并完成相应的任务：
克罗狄斯·托勒密（约90年～168年），是希腊数学家，天文学家，地理学家和占星家. 在数学方面，他还论证了四边形的特性，即有名的托勒密定理，托勒密定理的内容如下：圆的内接四边形的两条对角线的乘积等于两组对边乘积的和. 如图1，若四边形ABCD内接于⊙O，则有______.
任务：
（1）材料中横线上应填写的内容为__________；
（2）如图2，正五边形ABCDE内接于⊙O，AB = 2，求对角线BD的长.

答案： 解:
(1)AC·BD = AB·CD + AD·BC；
(2)连结 AD、AC.
∵五边形 ABCDE 是正五边形，
∴△ABC≌△DCB≌△AED，
∴AB = BC = CD = 2，AC = BD = AD，设 AC = BD = AD = x，在圆内接四边形 ABCD 中，由托勒密定理可得 AC·BD = AB·CD + AD·BC，即 $x^{2}=2\times2 + x\cdot2$，解得 $x_{1}=1+\sqrt{5}$，$x_{2}=1 - \sqrt{5}$(舍去)，
∴对角线 BD 的长为 $1+\sqrt{5}$.