2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10.已知函数y=(k - 3)x²+2x+1的图象与x轴有交点,则k的取值范围是( )
A. k<4
B. k≤4
C. k<4且k≠3
D. k≤4且k≠3
A. k<4
B. k≤4
C. k<4且k≠3
D. k≤4且k≠3
答案:
B
11.(2023自贡中考)经过A(2 - 3b,m),B(4b+c - 1,m)两点的抛物线y= - $\frac{1}{2}$x²+bx - b²+2c(x为自变量)与x轴有交点,则线段AB长为( )
A. 10
B. 12
C. 13
D. 15
A. 10
B. 12
C. 13
D. 15
答案:
B
12.(2023遂宁中考)抛物线y=ax²+bx+c(a≠0)的图象如图所示,对称轴为直线x= -2.下列说法:①abc<0;②c - 3a>0;③4a² - 2ab≥at(at+b)(t为全体实数);④若图象上存在点A($x_1$,$y_1$)和点B($x_2$,$y_2$),当m<$x_1$<$x_2$<m+3时,满足$y_1$=$y_2$,则m的取值范围为-5<m< -2,其中正确的个数有( )
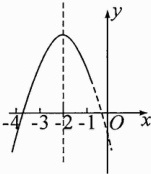
A. 1个
B. 2个
C. 3个
D. 4个
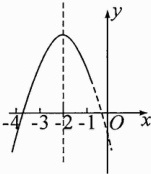
A. 1个
B. 2个
C. 3个
D. 4个
答案:
C
13.已知二次函数y=x²-2mx+m²+3(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?
答案:
(1)证明:$\because a = 1>0$,$\therefore$该函数的图象开口向上,又$\because y = x^{2}-2mx + m^{2}+3=(x - m)^{2}+3\geqslant 3$,$\therefore$该函数的图象在$x$轴上方,$\therefore$不论$m$为何值,该函数的图象与$x$轴没有公共点;
(2)沿$y$轴向下平移3个单位长度.
(1)证明:$\because a = 1>0$,$\therefore$该函数的图象开口向上,又$\because y = x^{2}-2mx + m^{2}+3=(x - m)^{2}+3\geqslant 3$,$\therefore$该函数的图象在$x$轴上方,$\therefore$不论$m$为何值,该函数的图象与$x$轴没有公共点;
(2)沿$y$轴向下平移3个单位长度.
14.已知二次函数y=x²+x+a的图象与x轴交于A($x_1$,0),B($x_2$,0)两点,且$\frac{1}{x_1^2}$+$\frac{1}{x_2^2}$=1,求a的值.
答案:
解:$\because$二次函数$y = x^{2}+x + a$的图象与$x$轴交于$A(x_{1},0)$,$B(x_{2},0)$两点,即$x_{1}$,$x_{2}$是方程$x^{2}+x + a = 0$的两实数根,$\therefore x_{1}+x_{2}=-1$,$x_{1}x_{2}=a$.$\therefore\frac{1}{x_{1}^{2}}+\frac{1}{x_{2}^{2}}=\frac{x_{1}^{2}+x_{2}^{2}}{x_{1}^{2}x_{2}^{2}}=\frac{(x_{1}+x_{2})^{2}-2x_{1}x_{2}}{(x_{1}x_{2})^{2}}=\frac{1 - 2a}{a^{2}} = 1$,$\therefore a=-1+\sqrt{2}$或$a=-1-\sqrt{2}$.$\because\Delta = 1 - 4\times 1\times a = 1 - 4a\geqslant 0$,$\therefore a\leqslant\frac{1}{4}$,$\therefore a=-1-\sqrt{2}$.
15.设a,b是任意两个实数,用max{a,b}表示a,b两数中较大者,例如:max{-1,1}=1,max{1,2}=2,max{4,3}=4.参照上面的材料,解答下列问题:
(1)max{5,2}=______,max{0,3}=______;
(2)若max{3x+1,-x+1}=-x+1,求x的取值范围;
(3)求函数y=x²-2x - 4与y=-x+2的图象的交点坐标,函数y=x²-2x - 4的图象如图所示,请你在图中作出函数y=-x+2的图象,并根据图象直接写出max{-x+2,x²-2x - 4}的最小值.

(1)max{5,2}=______,max{0,3}=______;
(2)若max{3x+1,-x+1}=-x+1,求x的取值范围;
(3)求函数y=x²-2x - 4与y=-x+2的图象的交点坐标,函数y=x²-2x - 4的图象如图所示,请你在图中作出函数y=-x+2的图象,并根据图象直接写出max{-x+2,x²-2x - 4}的最小值.

答案:
解:
(1)5;3;
(2)$\because\max\{3x + 1,-x + 1\}=-x + 1$,$\therefore 3x + 1\leqslant - x + 1$,解得$x\leqslant 0$;
(3)联立两函数解析式组成方程组$\begin{cases}y = x^{2}-2x - 4,\\y=-x + 2,\end{cases}$解得$\begin{cases}x_{1}=-2,\\y_{1}=4,\end{cases}\begin{cases}x_{2}=3,\\y_{2}=-1.\end{cases}$ $\therefore$交点坐标为$(-2,4)$和$(3,-1)$. 画出直线$y=-x + 2$略. 观察函数图象可知,当$x = 3$时,$\max\{-x + 2,x^{2}-2x - 4\}$取最小值 - 1.
(1)5;3;
(2)$\because\max\{3x + 1,-x + 1\}=-x + 1$,$\therefore 3x + 1\leqslant - x + 1$,解得$x\leqslant 0$;
(3)联立两函数解析式组成方程组$\begin{cases}y = x^{2}-2x - 4,\\y=-x + 2,\end{cases}$解得$\begin{cases}x_{1}=-2,\\y_{1}=4,\end{cases}\begin{cases}x_{2}=3,\\y_{2}=-1.\end{cases}$ $\therefore$交点坐标为$(-2,4)$和$(3,-1)$. 画出直线$y=-x + 2$略. 观察函数图象可知,当$x = 3$时,$\max\{-x + 2,x^{2}-2x - 4\}$取最小值 - 1.
查看更多完整答案,请扫码查看


