2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10.(2023宜宾中考)《梦溪笔谈》是我国古代科技著作,其中它记录了计算圆弧长度的“会圆术”.如图,$\overset{\frown}{AB}$是以点O为圆心、OA为半径的圆弧,N是AB的中点,MN⊥AB.“会圆术”给出$\overset{\frown}{AB}$的弧长l的近似值计算公式:l = AB + $\frac{MN^{2}}{OA}$.当OA = 4,∠AOB = 60°时,则l的值为( )
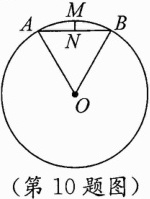
A.11 - 2$\sqrt{3}$
B.11 - 4$\sqrt{3}$
C.8 - 2$\sqrt{3}$
D.8 - 4$\sqrt{3}$

A.11 - 2$\sqrt{3}$
B.11 - 4$\sqrt{3}$
C.8 - 2$\sqrt{3}$
D.8 - 4$\sqrt{3}$
答案:
B
11.(2023成都中考)为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出.该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳______名观众同时观看演出.(π取3.14,$\sqrt{3}$取1.73)
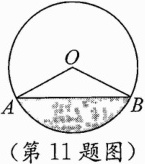

答案:
84
12.(广元中考)如图,将⊙O沿弦AB折叠,$\overset{\frown}{AB}$恰好经过圆心O,若AB = 2$\sqrt{3}$,则阴影部分的面积为________.
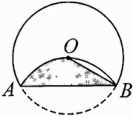

答案:
$\frac{2\pi}{3}$
13.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连结AC,BD.
(1)求证:AC = BD;
(2)若图中阴影部分的面积是$\frac{3}{4}\pi$cm²,OA = 2cm,求OC的长.
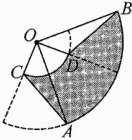
(1)求证:AC = BD;
(2)若图中阴影部分的面积是$\frac{3}{4}\pi$cm²,OA = 2cm,求OC的长.

答案:
(1)证明:
∵∠AOB = ∠COD = 90°,
∴∠AOC + ∠AOD = ∠BOD + ∠AOD,
∴∠AOC = ∠BOD.又AO = BO,CO = DO,
∴△AOC≌△BOD,
∴AC = BD;
(2)解:根据题意,得$S_{阴影}=\frac{90\pi OA^{2}}{360}-\frac{90\pi OC^{2}}{360}=\frac{90\pi(OA^{2}-OC^{2})}{360}$,
∴$\frac{3\pi}{4}=\frac{90\pi(2^{2}-OC^{2})}{360}$,解得OC = 1.
∴OC的长为1cm。
(1)证明:
∵∠AOB = ∠COD = 90°,
∴∠AOC + ∠AOD = ∠BOD + ∠AOD,
∴∠AOC = ∠BOD.又AO = BO,CO = DO,
∴△AOC≌△BOD,
∴AC = BD;
(2)解:根据题意,得$S_{阴影}=\frac{90\pi OA^{2}}{360}-\frac{90\pi OC^{2}}{360}=\frac{90\pi(OA^{2}-OC^{2})}{360}$,
∴$\frac{3\pi}{4}=\frac{90\pi(2^{2}-OC^{2})}{360}$,解得OC = 1.
∴OC的长为1cm。
14.如图,在等腰△ABC中,AB = AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DE = $\sqrt{3}$,∠C = 30°,求$\overset{\frown}{AD}$的长.

(1)求证:DE是⊙O的切线;
(2)若DE = $\sqrt{3}$,∠C = 30°,求$\overset{\frown}{AD}$的长.

答案:
(1)证明:连结OD,
∵OC = OD,AB = AC,
∴∠ODC = ∠C,∠C = ∠B,
∴∠ODC = ∠B,
∴OD//AB,
∵DE⊥AB,
∴DE⊥OD,又
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:连结AD,
∵AC为⊙O的直径,
∴∠ADC = 90°,即AD⊥BC,
∵AB = AC,
∴∠B = ∠C = 30°,BD = CD,
∵DE = $\sqrt{3}$,
∴BD = CD = 2$\sqrt{3}$,
∴OA = $\frac{1}{2}AC=\frac{1}{2}\times\frac{CD}{\cos30^{\circ}} = 2$,
∵∠AOD = 2∠C = 60°,
∴$\overset{\frown}{AD}$的长为$\frac{60\pi\times2}{180}=\frac{2\pi}{3}$。
(1)证明:连结OD,
∵OC = OD,AB = AC,
∴∠ODC = ∠C,∠C = ∠B,
∴∠ODC = ∠B,
∴OD//AB,
∵DE⊥AB,
∴DE⊥OD,又
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:连结AD,
∵AC为⊙O的直径,
∴∠ADC = 90°,即AD⊥BC,
∵AB = AC,
∴∠B = ∠C = 30°,BD = CD,
∵DE = $\sqrt{3}$,
∴BD = CD = 2$\sqrt{3}$,
∴OA = $\frac{1}{2}AC=\frac{1}{2}\times\frac{CD}{\cos30^{\circ}} = 2$,
∵∠AOD = 2∠C = 60°,
∴$\overset{\frown}{AD}$的长为$\frac{60\pi\times2}{180}=\frac{2\pi}{3}$。

15.(2023巴中中考)如图,已知等腰△ABC,AB = AC,以AB为直径作⊙O交BC于点D,过D作DF⊥AC于点E,交BA延长线于点F.
(1)求证:DF是⊙O的切线;
(2)若CE = $\sqrt{3}$,CD = 2,求图中阴影部分的面积(结果用π表示).
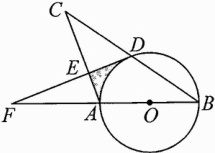
(1)求证:DF是⊙O的切线;
(2)若CE = $\sqrt{3}$,CD = 2,求图中阴影部分的面积(结果用π表示).

答案:
(1)证明:连结OD,
∵AB = AC,
∴∠B = ∠C,
∵OB = OD,
∴∠B = ∠ODB,
∴∠ODB = ∠C,
∴AC//OD,
∵DF⊥AC,
∴OD⊥DF,
∵OD是⊙O的半径,
∴DF是⊙O的切线;
(2)解:连结AD,设⊙O的半径为r,在Rt△CED中,CE = $\sqrt{3}$,CD = 2,
∴ED² = CD² - CE² = 4 - 3 = 1,
∴ED = 1,
∵cosC = $\frac{CE}{CD}=\frac{\sqrt{3}}{2}$,
∴∠C = 30°,
∴∠B = 30°,∠AOD = 60°,
∵AC//OD,O为AB的中点,
∴OD是△ABC的中位线,
∴D是BC中点,
∴CD = BD = 2,
∵AB是⊙O的直径,
∴∠ADB = 90°,
∴AD = $\frac{1}{2}AB = r$,
∴BD = $\sqrt{3}AD=\sqrt{3}r = 2$,
∴r = $\frac{2\sqrt{3}}{3}$,
∴AB = 2r = $\frac{4\sqrt{3}}{3}$,
∴AE = AC - CE = AB - $\sqrt{3}=\frac{4\sqrt{3}}{3}-\sqrt{3}=\frac{\sqrt{3}}{3}$,
∴阴影部分的面积 = 四边形AOED的面积 - 扇形AOD的面积 = $\frac{1}{2}\times(\frac{\sqrt{3}}{3}+\frac{2\sqrt{3}}{3})\times1-\frac{60\pi\times(\frac{2\sqrt{3}}{3})^{2}}{360}=\frac{\sqrt{3}}{2}-\frac{2\pi}{9}$。
(1)证明:连结OD,
∵AB = AC,
∴∠B = ∠C,
∵OB = OD,
∴∠B = ∠ODB,
∴∠ODB = ∠C,
∴AC//OD,
∵DF⊥AC,
∴OD⊥DF,
∵OD是⊙O的半径,
∴DF是⊙O的切线;
(2)解:连结AD,设⊙O的半径为r,在Rt△CED中,CE = $\sqrt{3}$,CD = 2,
∴ED² = CD² - CE² = 4 - 3 = 1,
∴ED = 1,
∵cosC = $\frac{CE}{CD}=\frac{\sqrt{3}}{2}$,
∴∠C = 30°,
∴∠B = 30°,∠AOD = 60°,
∵AC//OD,O为AB的中点,
∴OD是△ABC的中位线,
∴D是BC中点,
∴CD = BD = 2,
∵AB是⊙O的直径,
∴∠ADB = 90°,
∴AD = $\frac{1}{2}AB = r$,
∴BD = $\sqrt{3}AD=\sqrt{3}r = 2$,
∴r = $\frac{2\sqrt{3}}{3}$,
∴AB = 2r = $\frac{4\sqrt{3}}{3}$,
∴AE = AC - CE = AB - $\sqrt{3}=\frac{4\sqrt{3}}{3}-\sqrt{3}=\frac{\sqrt{3}}{3}$,
∴阴影部分的面积 = 四边形AOED的面积 - 扇形AOD的面积 = $\frac{1}{2}\times(\frac{\sqrt{3}}{3}+\frac{2\sqrt{3}}{3})\times1-\frac{60\pi\times(\frac{2\sqrt{3}}{3})^{2}}{360}=\frac{\sqrt{3}}{2}-\frac{2\pi}{9}$。
查看更多完整答案,请扫码查看


