《2025年智慧学堂九年级数学下册华师大版》

11.在Rt△ABC中，∠C = 90°，AC = 3，BC = 4，若以C为圆心，R为半径所作的圆与斜边AB只有一个公共点，则R的取值范围为________________.

答案： 3＜R≤4 或 R = 2.4

12.如图，⊙P的半径为2，点P在函数y = $\frac{6}{x}$(x＞0)的图象上运动，当x满足什么关系时，⊙P与x轴相切，相交，相离？

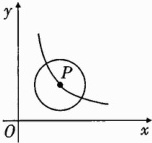
答案： 解:当⊙P 与 x 轴相切时,yP = 2,此时,xP = 3.
∴当 x = 3 时,⊙P 与 x 轴相切;当 x＞3 时,⊙P 与 x 轴相交;当 0＜x＜3 时,⊙P 与 x 轴相离.

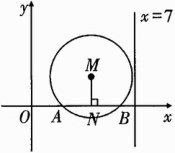
13.如图，在平面直角坐标系中，点M在第一象限内，MN⊥x轴于点N.MN = 1，⊙M与x轴交于A(2,0)，B(6,0)两点.
(1)求⊙M的半径；
(2)请判断⊙M与直线x = 7的位置关系，并说明理由.

答案： 解:
(1)连结 AM,M 为圆心,MN = 1,MN⊥x 轴于点 N,⊙M 与 x 轴交于点 A(2,0),B(6,0),
∴AN = NB = 1/2|2 - 6| = 2,AM =√(AN² + MN²)=√5.
∴⊙M 的半径为√5;
(2)相离. 理由如下:易知点 M 的横坐标为 4,其到直线 x = 7 的距离为 3,
∵3＞√5,
∴⊙M 与直线 x = 7 相离.

14.已知∠MAN = 30°，点O在AN上，以点O为圆心，2为半径作⊙O，交AN于点D，E，设AD = x.

(1)如图①，当x取何值时，直线AM与⊙O相切？
(2)如图②，当x取何值时，直线AM交⊙O于点B，C，且∠BOC = 90°？

答案： 解:
(1)过点 O 作 OF⊥AM,垂足为 F. 当 OF = r = 2 时,直线 AM 与⊙O 相切,此时易知 OA = 4,故 AD = 2,即当 x = 2 时,直线 AM 与⊙O 相切;
(2)过点 O 作 OG⊥BC,垂足为 G,则 BG = CG,
∵OB = OC = 2,∠BOC = 90°,
∴BC =√(OB² + OC²)=√(2² + 2²)= 2√2,
∴BG = CG =√2,
∴OG =√2,
∵∠A = 30°,
∴OA = 2√2,
∴AD = OA - OD = 2√2 - 2,即当 x = 2√2 - 2 时,直线 AM 交⊙O 于点 B,C,且∠BOC = 90°.

15.(重庆渝中模拟)阅读理解：
在平面直角坐标系xOy中，点P(x₀,y₀)到直线Ax + By + C = 0(A² + B²≠0)的距离公式：d = $\frac{\vert Ax_{0}+By_{0}+C\vert}{\sqrt{A^{2}+B^{2}}}$，例如，求点P(1,3)到直线4x + 3y - 3 = 0的距离.
解：由直线4x + 3y - 3 = 0可知A = 4，B = 3，C = -3，故P(1,3)到直线4x + 3y - 3 = 0的距离d = $\frac{\vert 4\times1 + 3\times3 - 3\vert}{\sqrt{4^{2}+3^{2}}}$ = 2.
根据以上材料，解决下列问题：
(1)求点P₁(1,-1)到直线3x - 4y - 2 = 0的距离；
(2)在(1)的基础上，若以点P₁为圆心，2为半径作圆，请直接写出直线与圆的位置关系.

答案： 解:
(1)点 P1(1, - 1)到直线 3x - 4y - 2 = 0 的距离 d = |3×1 - 4×( - 1) - 2|/√(3² + ( - 4)²)= 1;
(2)
∵点 P1 到直线 3x - 4y - 2 = 0 的距离为 1,圆 P1 的半径为 2,
∴直线与圆 P1 的位置关系是相交.