2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 在⊙O中,M,N分别为弦AB,CD的中点,如果AB = CD,那么在结论:①OM = ON;②AB = CD;③∠AOB = ∠COD中,正确的是( )
A. ①②
B. ①③
C. ②③
D. ①②③
A. ①②
B. ①③
C. ②③
D. ①②③
答案:
D
11. 如图,⊙O在△ABC三边上截得的弦长都相等,∠A = 80°,则∠BOC的度数为________.
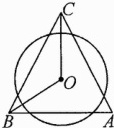

答案:
$130^{\circ}$
12. 如图,分别过⊙O的直径AB上的点M,N作弦CD,EF,若CD//EF,AC = BF. 求证:
(1)BEC = ADF;
(2)AM = BN.
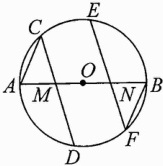
(1)BEC = ADF;
(2)AM = BN.

答案:
证明:
(1)连结$OC$,$OF$.
∵$AC = BF$,
∴$∠COA = ∠BOF$,
∴$∠COB = ∠FOA$,
∴$\overset{\frown}{BEC}=\overset{\frown}{ADF}$;
(2)
∵$∠COA = ∠BOF$,$OC = OF = OA = OB$,
∴$∠CAB = ∠ACO = \frac{1}{2}(180^{\circ}-∠COA)$,$∠BFO = ∠ABF = \frac{1}{2}(180^{\circ}-∠BOF)$,
∴$∠CAB = ∠ABF$,
∵$CD// EF$,
∴$∠AMC = ∠ANE$,又
∵$∠BNF = ∠ANE$,
∴$∠AMC = ∠BNF$,又
∵$AC = BF$,
∴$\triangle AMC\cong\triangle BNF$(AAS),
∴$AM = BN$.
(1)连结$OC$,$OF$.
∵$AC = BF$,
∴$∠COA = ∠BOF$,
∴$∠COB = ∠FOA$,
∴$\overset{\frown}{BEC}=\overset{\frown}{ADF}$;
(2)
∵$∠COA = ∠BOF$,$OC = OF = OA = OB$,
∴$∠CAB = ∠ACO = \frac{1}{2}(180^{\circ}-∠COA)$,$∠BFO = ∠ABF = \frac{1}{2}(180^{\circ}-∠BOF)$,
∴$∠CAB = ∠ABF$,
∵$CD// EF$,
∴$∠AMC = ∠ANE$,又
∵$∠BNF = ∠ANE$,
∴$∠AMC = ∠BNF$,又
∵$AC = BF$,
∴$\triangle AMC\cong\triangle BNF$(AAS),
∴$AM = BN$.
13. 如图,AB是⊙O的直径,AC = CD,∠COD = 60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC//BD.
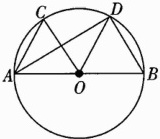
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC//BD.

答案:
(1)解:$\triangle AOC$是等边三角形. 理由:
∵$\overset{\frown}{AC}=\overset{\frown}{CD}$,
∴$∠AOC = ∠COD = 60^{\circ}$. 又
∵$OA = OC$.
∴$\triangle AOC$是等边三角形;
(2)证明:
∵$\overset{\frown}{AC}=\overset{\frown}{CD}$,
∴$∠AOC = ∠COD = 60^{\circ}$,
∴$∠BOD = 180^{\circ}-(∠AOC + ∠COD)= 60^{\circ}$.
∵$OD = OB$,
∴$\triangle ODB$为等边三角形.
∴$∠OBD = 60^{\circ}$,
∵$∠OBD = ∠AOC = 60^{\circ}$,
∴$OC// BD$.
(1)解:$\triangle AOC$是等边三角形. 理由:
∵$\overset{\frown}{AC}=\overset{\frown}{CD}$,
∴$∠AOC = ∠COD = 60^{\circ}$. 又
∵$OA = OC$.
∴$\triangle AOC$是等边三角形;
(2)证明:
∵$\overset{\frown}{AC}=\overset{\frown}{CD}$,
∴$∠AOC = ∠COD = 60^{\circ}$,
∴$∠BOD = 180^{\circ}-(∠AOC + ∠COD)= 60^{\circ}$.
∵$OD = OB$,
∴$\triangle ODB$为等边三角形.
∴$∠OBD = 60^{\circ}$,
∵$∠OBD = ∠AOC = 60^{\circ}$,
∴$OC// BD$.
14. 问题呈现:阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是ABC的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD = AB + BD. 下面是运用“截长法”证明CD = AB + BD的部分证明过程.
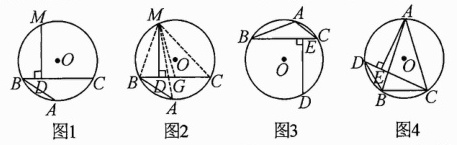
证明:如图2,在CB上截取CG = AB,连结MA,MB,MC和MG. ∵M是ABC的中点,∴MA = MC. 易得∠A = ∠C(同弧所对的圆周角相等)……
请按照上面的证明思路,写出该证明的剩余部分.
实践应用:
(1)如图3,已知△ABC内接于⊙O,BC>AB>AC,D是ACB的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为________;
(2)如图4,已知等腰△ABC内接于⊙O,AB = AC,D为AB上一点,连结DB,CD,∠ACD = 45°,AE⊥CD于点E,△BCD的周长为4$\sqrt{2}$ + 2,BC = 2,请求出AC的长.

证明:如图2,在CB上截取CG = AB,连结MA,MB,MC和MG. ∵M是ABC的中点,∴MA = MC. 易得∠A = ∠C(同弧所对的圆周角相等)……
请按照上面的证明思路,写出该证明的剩余部分.
实践应用:
(1)如图3,已知△ABC内接于⊙O,BC>AB>AC,D是ACB的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为________;
(2)如图4,已知等腰△ABC内接于⊙O,AB = AC,D为AB上一点,连结DB,CD,∠ACD = 45°,AE⊥CD于点E,△BCD的周长为4$\sqrt{2}$ + 2,BC = 2,请求出AC的长.
答案:
问题呈现:证明:如图2,在$CB$上截取$CG = AB$,连结$MA$,$MB$,$MC$和$MG$.
∵$M$是$\overset{\frown}{ABC}$的中点,
∴$MA = MC$. 易得$∠A = ∠C$(同弧所对的圆周角相等). 在$\triangle MBA$和$\triangle MGC$中,$\begin{cases}∠A = ∠C, \\ MA = MC, \\ AB = GC,\end{cases}$
∴$\triangle MBA\cong\triangle MGC$,
∴$MB = MG$,又
∵$MD\perp BC$,
∴$BD = GD$,
∴$CD = GC + GD = AB + BD$. 实践应用:解:
(1)$BE = CE + AC$;
(2)
∵$AB = AC$,
∴$A$是$\overset{\frown}{BAC}$的中点,
∴$AE\perp BC$,根据阿基米德折弦定理得,$CE = BD + DE$,
∵$\triangle BCD$的周长为$4\sqrt{2}+2$,
∴$BD + CD + BC = 4\sqrt{2}+2$,
∴$BD + DE + CE + BC = 2CE + BC = 4\sqrt{2}+2$,
∵$BC = 2$,
∴$CE = 2\sqrt{2}$,在$Rt\triangle ACE$中,
∵$∠ACE = 45^{\circ}$,
∴$AE = CE = 2\sqrt{2}$,
∴$AC = 4$.
∵$M$是$\overset{\frown}{ABC}$的中点,
∴$MA = MC$. 易得$∠A = ∠C$(同弧所对的圆周角相等). 在$\triangle MBA$和$\triangle MGC$中,$\begin{cases}∠A = ∠C, \\ MA = MC, \\ AB = GC,\end{cases}$
∴$\triangle MBA\cong\triangle MGC$,
∴$MB = MG$,又
∵$MD\perp BC$,
∴$BD = GD$,
∴$CD = GC + GD = AB + BD$. 实践应用:解:
(1)$BE = CE + AC$;
(2)
∵$AB = AC$,
∴$A$是$\overset{\frown}{BAC}$的中点,
∴$AE\perp BC$,根据阿基米德折弦定理得,$CE = BD + DE$,
∵$\triangle BCD$的周长为$4\sqrt{2}+2$,
∴$BD + CD + BC = 4\sqrt{2}+2$,
∴$BD + DE + CE + BC = 2CE + BC = 4\sqrt{2}+2$,
∵$BC = 2$,
∴$CE = 2\sqrt{2}$,在$Rt\triangle ACE$中,
∵$∠ACE = 45^{\circ}$,
∴$AE = CE = 2\sqrt{2}$,
∴$AC = 4$.
查看更多完整答案,请扫码查看


