《2025年智慧学堂九年级数学下册华师大版》

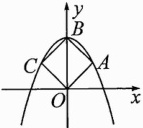
10. 如图，抛物线$y = ax^{2}+c$经过正方形$OABC$的三个顶点$A、B、C$，点$B$在$y$轴上，则$ac$的值为（ ）

A. -1
B. -2
C. -3
D. -4

答案： B

11. 在同一坐标系中，一次函数$y=-mx + n^{2}$与二次函数$y = x^{2}+m$的图象可能是（ ）

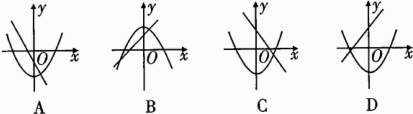
答案： D

12.（重庆一中月考）对于二次函数$y = 2x^{2}-3$，当$-1\leqslant x\leqslant2$时，$y$的取值范围是（ ）
A. $-1\leqslant y\leqslant5$
B. $-5\leqslant y\leqslant5$
C. $-3\leqslant y\leqslant5$
D. $-2\leqslant y\leqslant5$

答案： C

13. 若抛物线$y = 2x^{m^{2}-4m - 3}+m - 5$的顶点在$x$轴的下方，则$m =$_______. 若二次函数$y=(k + 1)x^{2}+k^{2}-k$的图象的顶点坐标为$(0,2)$，则$k =$_______.

答案： -1;2

14. 把$y=-\frac{1}{2}x^{2}$的图象向上平移2个单位.
（1）求新图象的表达式、顶点坐标和对称轴；
（2）在对称轴右侧部分，$y$随$x$的增大怎样变化？
（3）求函数的最大值或最小值，并求对应的$x$的值.

答案： 解:
(1)y = -$\frac{1}{2}$x²+2,顶点坐标是(0,2),对称轴是y轴;
(2)在对称轴右侧部分,y随x的增大而减小;
(3)x = 0时,y有最大值,为2.

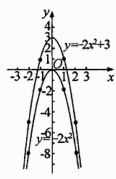
15. 如图，在平面直角坐标系中，抛物线$y = ax^{2}+3$与$y$轴交于点$A$，过点$A$与$x$轴平行的直线交抛物线$y=\frac{1}{3}x^{2}$于点$B$，$C$.
（1）求$BC$的长度；
（2）点$A_{1}(\sqrt{2},y_{1})$，$A_{2}(5,y_{2})$，$A_{3}(-\sqrt{5},y_{3})$，都在抛物线$y = ax^{2}+3$上，试比较$y_{1}$、$y_{2}$、$y_{3}$的大小.

答案： 解:
(1)由题意得A(0,3),令y = $\frac{1}{3}$x² = 3,
∴x₁ = 3,x₂ = -3,
∴BC = 3 - (-3)=6;
(2)|$\sqrt{2}$|＜| - $\sqrt{5}$|＜|5|且a＜0,
∴y₁ ＞y₃＞y₂.

16. 如图，已知正比例函数$y = 2x$的图象与抛物线$y = ax^{2}+3$相交于点$A(1,b)$.
（1）求$a$与$b$的值；
（2）若点$B(m,4)$在函数$y = 2x$的图象上，抛物线$y = ax^{2}+3$的顶点是$C$，求$\triangle ABC$的面积；
（3）若$P$是$x$轴上一个动点，求当$PA+PC$最小时点$P$的坐标.

答案：
解:
(1)把点A(1,b)的坐标代入y = 2x,得b = 2,
∴A(1,2).把点A(1,2)的坐标代入y = ax²+3,得a = -1;
(2)把点B(m,n)的坐标代入y = 2x,得m = 2,
∴B(2,4),
∵抛物线y = ax²+3的顶点C的坐标是(0,3),
∴OC = 3,
∴S△ABC = S△OBC - S△OAC = $\frac{1}{2}$×OC×2 - $\frac{1}{2}$×OC×1 = $\frac{1}{2}$×3×2 - $\frac{1}{2}$×3×1 = $\frac{3}{2}$;
(3)设点C关于x轴的对称点为C',则C'的坐标为(0,-3),连接AC'与x轴交于点P,此时PA + PC最小.设直线AC'的函数解析式是y = kx + n,把C'(0,-3),A(1,2)的坐标代入,得$\begin{cases}n=-3\\k + n = 2\end{cases}$,解得$\begin{cases}k = 5\\n=-3\end{cases}$,
∴y = 5x - 3.当y = 0时,5x - 3 = 0,
∴x = $\frac{3}{5}$,
∴点P的坐标是($\frac{3}{5}$,0).