《2025年智慧学堂九年级数学下册华师大版》

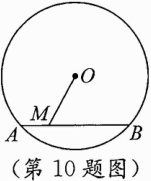
10.如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段OM的长的取值范围是（ ）

A.3≤OM≤5
B.4≤OM≤5
C.3＜OM＜5
D.4＜OM＜5

答案： B

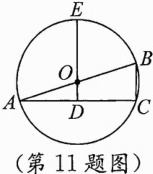
11.(泸州中考)如图，AB是⊙O的直径，OD垂直于弦AC于点D，DO的延长线交⊙O于点E.若AC=4$\sqrt{2}$，DE=4，则BC的长是（ ）

A.1
B.$\sqrt{2}$
C.2
D.4

答案： C

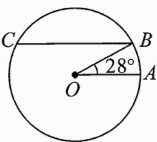
12.(遵义中考)数学小组研究如下问题：遵义市某地的纬度约为北纬28°，求北纬28°纬线的长度.小组成员查阅相关资料，得到如下信息：信息一：在地球仪上，与赤道平行的圆圈叫做纬线；信息二：如图，赤道半径OA约为6400千米，弦BC//OA，求BC为直径的圆的周长就是北纬28°纬线的长度；根据以上信息，北纬28°纬度的长度约为________千米.(参考数据：π≈3，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53)

答案： 33792

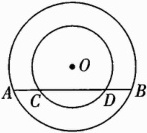
13.已知在以O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D(如图所示).
(1)求证：AC=BD；
(2)若大圆的半径R=10，小圆的半径r=8，且圆心O到直线AB的距离为6，求AC的长.

答案：
(1)证明:过点O作OE⊥AB于点E. 则CE = DE,AE = BE,
∴AE - CE = BE - DE,即AC = BD;
(2)解:连结OA,OC,由
(1)可知,OE⊥AB,且OE⊥CD,
∴CE = $\sqrt{OC^{2}-OE^{2}}=\sqrt{8^{2}-6^{2}} = 2\sqrt{7}$,AE = $\sqrt{OA^{2}-OE^{2}}=\sqrt{10^{2}-6^{2}} = 8$,
∴AC = AE - CE = 8 - 2\sqrt{7}.

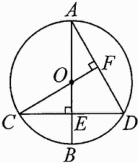
14.(2023成都七中育才学校月考)如图，已知圆O的直径AB垂直弦CD于点E，连结CO并延长交AD于点F，且CF⊥AD.
(1)求证：点E是OB的中点；
(2)若AB=8，求CD的长.

答案：
(1)证明:连结AC.
∵直径AB垂直弦CD于E,
∴CE = DE,∠AEC = ∠AED = 90°,又
∵AE = AE,
∴△AEC≌△AED(SAS),
∴AC = AD,
∵过圆心O的线段CF⊥AD,
∴AF = DF,即CF是AD的垂直平分线,
∴AC = CD,
∴AC = AD = CD,即△ACD是等边三角形,
∴∠FCD = 30°,
∴在Rt△COE中,OE = $\frac{1}{2}$OC,又
∵OC = OB,
∴OE = $\frac{1}{2}$OB,即点E是OB的中点;
(2)解:
∵AB = 8,
∴OC = OB = $\frac{1}{2}$AB = 4,又
∵BE = OE,
∴OE = 2,在Rt△OCE中,CE = $\sqrt{OC^{2}-OE^{2}}=\sqrt{4^{2}-2^{2}} = 2\sqrt{3}$,又
∵CE = DE,
∴CD = 2CE = 4\sqrt{3}.

15.如图，在半径为5的扇形AOB中，∠AOB=90°，点C是$\overset{\frown}{AB}$上的一个动点(不与点A，B重合)，OD⊥BC，OE⊥AC，垂足分别为点D，E.
(1)当BC=6时，求线段OD的长；
(2)在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由.

答案： 解:
(1)
∵OD⊥BC,
∴BD = $\frac{1}{2}$BC = 3. 在Rt△BOD中,OD = $\sqrt{OB^{2}-BD^{2}}=\sqrt{5^{2}-3^{2}} = 4$;
(2)存在. DE的长度保持不变,连结AB,
∵OD⊥BC,OE⊥AC,
∴点D,E分别为BC,AC中点,
∴DE为△ABC的中位线,
∴DE = $\frac{1}{2}$AB = $\frac{1}{2}\times\sqrt{5^{2}+5^{2}}=\frac{5\sqrt{2}}{2}$.